INTRO
1) 추정과 검정의 차이
추정 - 예측 - 보통 큰 회사에서 한다. 단지 조금 빨리 알기 위해 하는 경우가 많다. ex> 대선, 수능 등급컷
(그래서 우리에게 추정의 중요도가 조금 떨어질 수 있다.)
검정 - 주장 - 일상 속에서도 할 수 있다.
2) 검정의 기본 원리 (3단계)
1> 가설 설정(주장) - 2> 통계적 계산 - 3> 결론 (SAS는 통계적 계산을 하지만 우리는 주장과 결론 부분을 담당한다.)
1. 가설 설정의 기본 원리
1) 기본 개념
1> 귀무가설 (H0) : 기각을 전제로 세우는 가설
(중요하다. 가설 검정은 내가 주장하는 것이다. 어떤 상황일 때 주장하고 싶을까? 그에 대해 반하는 생각을 가질 때 주장한다.)
- 실제로 알려져 있는 사실 (지금까지 알려진 학설)
- 하지만 내가 반대할 가설
2> 대립가설 (H1) : 귀무가설이 기각될 때 상대적으로 채택되는 가설
- 나의 주장
- 그래서 실험할 때 목표가 있다면 그 목표를 대립가설에 넣고 시작하자.
3> 통계적 검정 : 표본의 정보를 기초로 주어진 가설을 기각 할 것인지 아닌지 결정하는 절차
- 분포에서의 위치를 기준으로 검정
- 그래서 검정에서는 원래 무슨 분포였는지 아는 게 중요하다.
4> 검정의 기각역 : 귀무가설 (H0)이 기각 되는 영역
- 우리 입장에서는 귀무가설을 기각하는 것이 좋다.
- 그래서 귀무 가설의 기각역을 찾는다.
- 이 검정을 통해 이 영역 안으로 들어가는 것을 목표로 할 것이다.
2) 검정의 오류, 유의 수준

1> α
- 정의 : H0가 참이지만 H0를 기각했다.
- 추정에 나온 α와 같은 의미이다.
2> β
- 정의 : H0가 거짓이지만 H0를 채택했다.
(α와 β는 trade-off 관계)
3> 방법 1 : α만 가지고 검정
- 둘 중 하나는 무시 -> 다루기 쉬운 오류만 줄여본다 -> 어떤 게 다루기 쉬운지 결정하기
-> H0가 참이라는 전제하에 계산하는 α가 계산하기 편하다.
4> 방법 2 : α를 고정시킨 상태에서 β가 가장 작은 상태를 찾는다.
- 1-β는 검정역 (최강 검정역을 찾는다.)
2. 정규 분포에 관한 검정 - 단일 표본
0) 모평균(μ) 추정
1> σ^2를 아는 경우 => 표준 정규 분포 (중심 극한 정리를 사용하면 되니까 정규성 가정이 없어도 된다.)
2> σ^2를 모르는 경우 => t-분포
1) 모평균(μ)에 관한 검정 - 모분산(σ)을 아는 경우
(극히 드문 case)

1> n >= 30 이거나 정규성 가정이 있어야 한다.
2> 표준화를 진행해서 Z를 만든다.
3> 귀무 가설이 맞다고 가정하고 귀무 가설 H0에 해당하는 모평균 μ0을 가지고 통계량 z0를 만든다.
=> z0는 상수가 나온다.

[(1)번처럼 '모평균 μ >귀무가설 평균 μ0'을 대립 가설로 주장하는 예시]
우리가 계산한 표본 평균 x^을 모평균처럼 여겨본다.
=> 우리가 예측한 통계량(표본 평균 x^)이 μ0보다 커야한다.
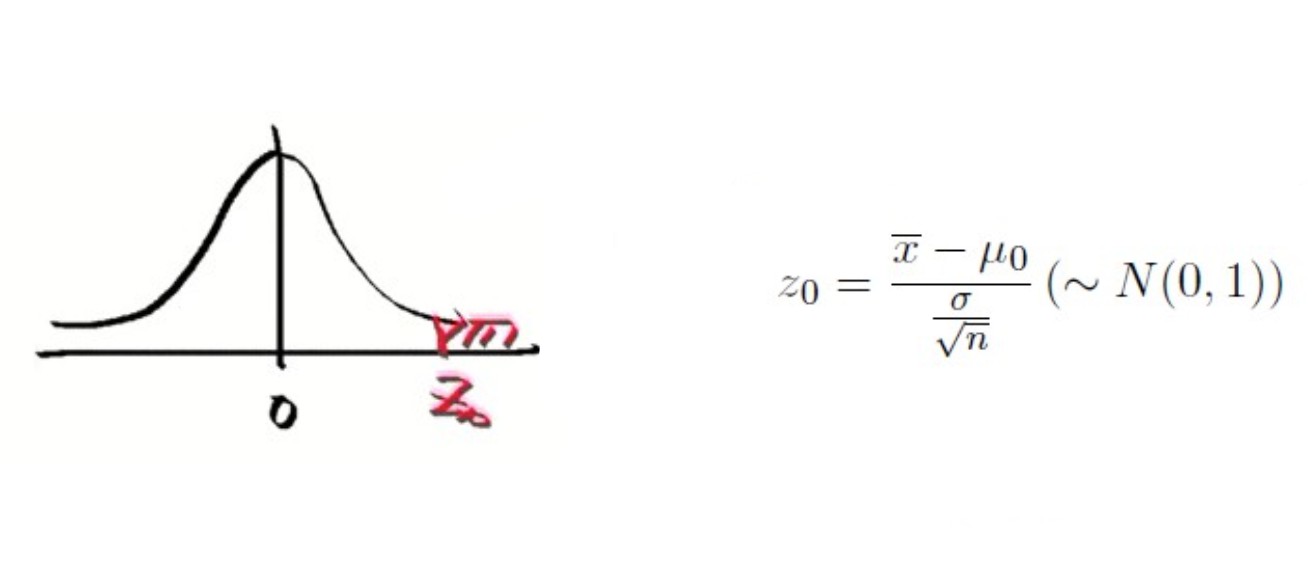
4> 그림을 그려본다. -> x^가 μ0보다 커야한다. -> z0가 양수로 나온다. -> z0가 중앙에서 오른쪽으로 멀리 떨어질수록 좋다.
5> 그럼 얼마나 z0가 커야하는가? 기준이 유의 수준 α이다.
=> z0가 α 범위 안으로 들어오도록 하자 -> P(Z>= z0) > α -> Z_0 > Z_α
6> 결론 : 유의 수준이 검정 통계량보다 커야 한다.
=> 유의 수준과 검정 통계량을 비교한다.
=> '유의 수준 = 확률', '검정 통계량 = x축 위의 점'
=> 바로 비교할 수 없다.
=> α를 x축 위의 점으로 변환 (α -> Z_α)
7> (2)의 경우
=> 이번에도 z0가 중앙에서 멀리 떨어져야 한다.
=> 하지만 상위 누적 확률을 이용하기 때문에
=> 반대로 생각하면 z0의 x좌표가 α의 위치보다 뒤에 있어야 한다.
=> z0의 상위 확률이 α의 상위 확률보다 커야 한다. (그리고 α의 상위 확률은 음수 변환을 한다.)
=> Z_0 < -Z_α
8> (3)의 경우
=> 이번에도 z0가 중앙에서 멀리 떨어져야 한다.
=> 오른쪽은 z0의 상위 확률이 α의 상위 확률보다 커야 한다.
=> Z_0 > Z_α/2
=> 반대는 Z_0 < -Z_α/2.
=> 결론 : |Z_0| > Z_α/2
2) 모평균(μ)에 관한 검정 - 모분산(σ)을 모르는 경우

1> 정규성 가정이 있어야 한다.
2> 표준화와 달리 모분산 부분을 표본 분산으로 대체해서 연산한 결과 T를 구한다.
3> 귀무 가설이 맞다고 가정하고 귀무 가설 H0에 해당하는 모평균 μ0을 가지고 통계량 z0를 만든다.
=> z0는 상수가 나온다.

※ 주의 : 자유도는 n-1이다. (표본 분산으로 인해 분모 카이-제곱의 자유도가 n-1이기 때문이다.)
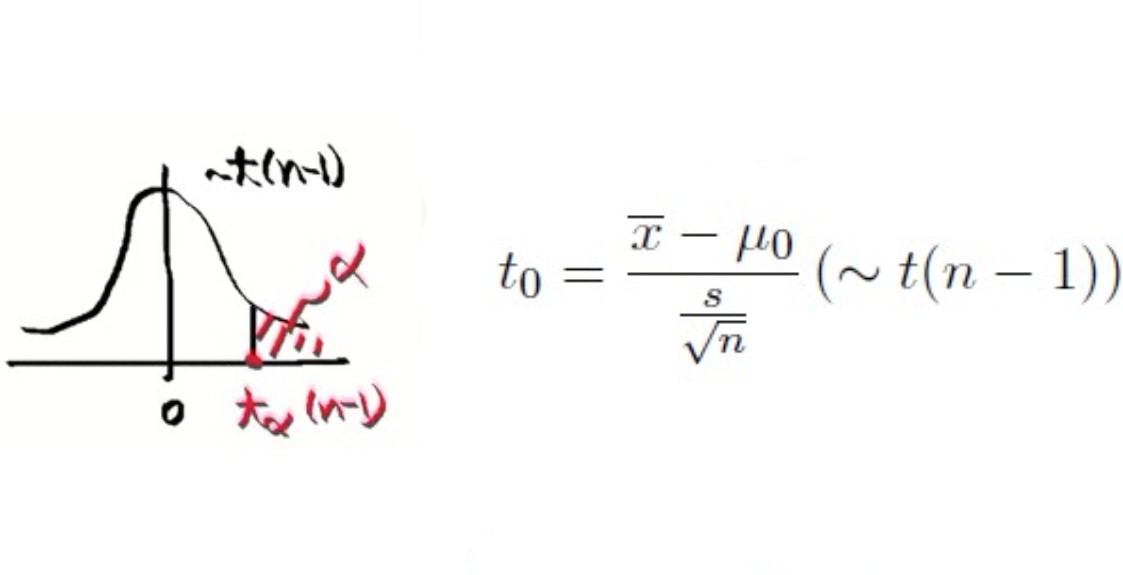
4> 1)의 원리대로 t0(x좌표)가 중앙에서 멀리 떨어져 α(확률)의 범위 안으로 들어오게 한다.
3) 모비율(p)에 관한 검정

1> 추정과 달리 분모에 p^이 없다.

=> 검정의 경우 H0가 사실이라는 전제 하에 검정하는 것이므로 원래(추정 이전) p의 자리에 p0를 넣으면 된다.

3. 정규 분포에 관한 검정 실습 - 단일 표본
1) 모평균에 관한 검정 - PROC TTEST 이용
(실제로 σ을 아는 경우가 드물기 때문에 t-분포를 이용한 실습만 진행합니다.)
1> PROC TTEST
- 모평균에 관한 검정, 모평균 차에 관한 검정, 짝표본 검정등 t-검정이 모두 가능한 프로시저
- H0=m이라는 명령어를 사용하여 귀무가설을 설정할 수 있고, 이를 설정하지 않으면 H0=0로 설정이 된다.
- PROC TTEST data=SAS-dataset H0=μ0 : 귀무가설인 모평균 μ0를 원하는 값으로 설정한다.
2> 예시

- DF : 자유도
- t Value : 검정 통계량
- 하지만 우측 검정, 좌측 검정, 양측 검정을 선택하지 못한다. 그래서 직접 표를 보고 계산해야 한다.
- Pr > |t| : 확률이 t(검정 통계량)의 절댓값보다 클 확률 = 양측 검정의 p-value (PROC TEST의 defualt는 양측 검정이다.)
=> 유의 수준을 0.3273을 잡아야 하는데 그만큼 잡을 수 없다. (10%로도 못 잡는다.)
그러면 우측 검정이나 촤측 검정은 어떻게 하느가?
- 첫 번째 그래프
TTEST는 정규성 가정이 필요하다. 하지만 정규 분포를 가지지 않음에도 일단 TTEST를 진행해본다.
그 결과 첫 번째 그래프에서는 정규성을 검증해 볼 수 있게 실제 정규 분포와 현재 그래프를 동시에 출력한다.
- 두 번째 그래프 (Q-Q plot)
※ 유의 확률 (p-value)
유의 수준이 작은 것도 중요하지만 기각하는 것이 더 중요하다.
이전에는 주어진 유의 수준에서 기각할 수 있는지만 확인했다.
이번에는 유의 수준을 고정시키지 말고 유의 수준을 얼마까지 높이면 기각할 수 있는지 알아본다.
1) 정의 및 특징
1> 유의 확률 : 귀무가설을 기각할 수 있는 최소한의 확률 (p값, p-value)
2> p보다 크면 기각할 수 있다. => p는 작을수록 좋다.
3> 가설이 다르면 유의 확률도 달라진다.
2) 구하는 방법 (t분포로 설명)
[우측 검정]
1> 검정 통계량 t0를 구한다.

2> α(확률, 면적)가 t0(x축)을 포함해야 한다. => P[T > t0] = p0 (x축인 t0를 확률로 변환)
3> α >= (P[T > t0] = p0) => H0를 기각한다.
2) 모평균에 관한 검정 - PROC UNIVARIATE 이용
1> PROC UNIVARIATE
- 모평균에 관한 검정, 모평균 차에 관한 검정, 짝표본 검정등 t-검정이 모두 가능한 프로시저
- mu0=m이라는 명령어를 사용하여 귀무가설을 설정할 수 있고, 이를 설정하지 않으면 H0=0로 설정이 된다.
- PROC UNIVARIATE data=SAS-dataset mu0=μ0 alpha=α cibasic: 귀무가설인 모평균 μ0를 원하는 값으로 설정한다.
2> 예시 1
DATA csi;
INPUT csi @@;
LABEL csi='소비자 만족도 지수';
CARDS;
75 63 49 86 53 80 70 72 81 80 69 76 85 95 66 77 77 63 58 74
68 90 82 59 60
;
RUN;
proc univariate data=csi mu0=70 alpha=0.05 cibasic;
var csi;
run;
- cibasic : confidence interval basic => 그래서 alpha 옵션을 써주어야 한다.
- alpha=0.05 cibasic : 신뢰구간을 구할 수 있다. (검정만 하고 싶다면 쓰지 않아도 된다.)

- mu0=70 : 귀무가설에서 평균을 70으로 설정

- 이번에도 양측 검정이 p-value만 출력된다.
- t-value(t0)가 1
3> 예시 2 (mu0 설정을 data에서 진행)
DATA csi;
INPUT csi @@;
LABEL csi='소비자 만족도 지수';
csi1=csi-70; /*mu0=70 설정하는 효과*/
CARDS;
75 63 49 86 53 80 70 72 81 80 69 76 85 95 66 77 77 63 58 74
68 90 82 59 60
;
RUN;
proc univariate data=csi alpha=0.05 cibasic; /*mu0=70 설정을 여기서 안 해도 된다.*/
var csi1;
run;
3) 모비율에 관한 검정 - PROC FREQ 이용
Bernoulli분포에서는 ~이다, ~ 아니다. => PROC FREQ
1> PROC FREQ
- tables 명령어 옵션 중 binomial (p=p0)를 사용 => 귀무 가설(H0) 설정
2> 예시

<이전 FREQ 복습>
(이 그림에서는 state가 범주가 되고, count를 뽑힌 횟수로 취급할 것입니다.)
- data=SAS-dataset : 사용할 data 선정
- order=data : 데이터에 제시된 순서대로 분석할 지 => 데이터에서 가장 먼저 나타나는 범주을 대상으로 분석
- weight variable_count : 정렬되어 있는 경우(현재 상황) 이 변수의 숫자를 뽑힌 횟수로 취급
- tables variable_category / binomial (p=p0) alpha=α :
- 이항비 table을 variable을 범주로해서 만든다. (variable_category에 대한 이항비 table)
- α는 추후 신뢰구간을 만들 경우 사용할 수 있다.
- 검정 결과
- Z = 검정 통계량
- 단측 pr < Z : (Z가 음수이기도 해서) 좌측 검정에 대한 p-value
'SAS' 카테고리의 다른 글
| [통계 개념&SAS] 8-3강 - 가설 검정 (독립인 모집단이 2개인 경우) (0) | 2020.05.12 |
|---|---|
| [통계 개념&SAS] 8-2강 - 유의 확률 (p-value) (0) | 2020.05.07 |
| [통계 개념] 7-5강 - 모집단이 2개인 경우 통계량 차에 대한 구간 추정 (신뢰 구간) (0) | 2020.05.07 |
| [SAS] 7-4강 - 점 추정, 구간 추정 실습 (0) | 2020.05.07 |
| [통계 개념] 7-3강 - 구간 추정 : 신뢰 구간 (0) | 2020.05.07 |



