분포와 관련 없이 표본 평균은 모평균의 불편 추정량, 표본 분산은 모분산의 불편 추정량이다. (표본 비율도 마찬가지)
실제 점 추정을 할 경우 기술 통계량을 나타내주는 procedure 이용 => PROC UNIVARIATE, MEANS, SUMMARY
모비율에 대한 점 추정을 할 경우 횟수를 세야 한다. => PROC FREQ
4. 모평균과 모분산에 대한 점 추정, 구간 추정 1 (UNIVARIATE)
0) CIBASIC 사용
1> CIBASIC = confiedence interval basic = 기본 방법으로 신뢰 구간을 구한다.
2> 신뢰 구간을 구하기 위해서는 유의 수준(α)를 알아야 한다. => 그래서 'ALPHA = '를 옵션으로 유의 수준을 설정한다.
1) 문법
1> 추가된 것
- PROC UNIVARIATE data=SAS-dataset cibasic alpha=유의 수준(α);
2) 예시
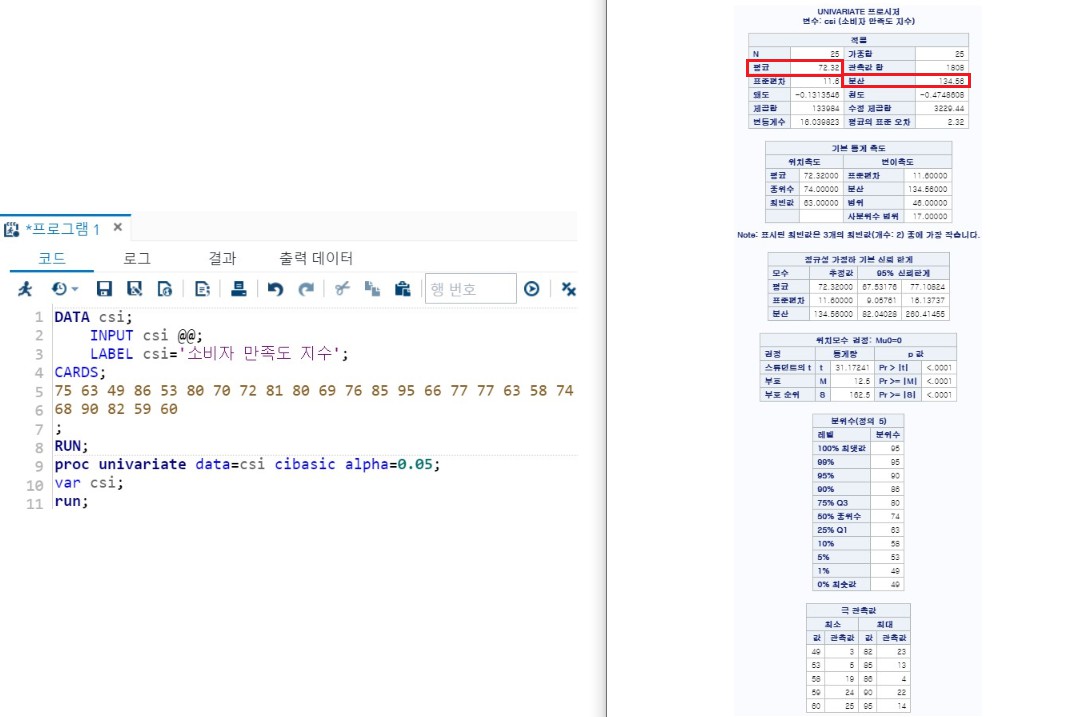
1> 점 추정 (평균, 분산)
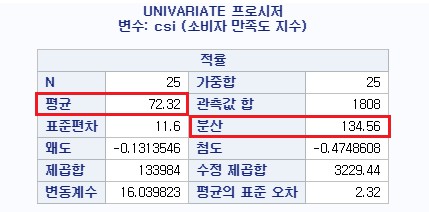
- LABEL을 따로 붙였기 때문에 맨 위에 '변수 : csi (소비자 만족도 지수)'가 나온다.
- 결과에서 '평균'이 표본 평균이므로 72.32가 평균에 대한 점 추정이다.
- 결과에서 '분산'이 표본 분산이므로 134.56이 분산에 대한 점 추정
cf> 원래 평균에 대한 구간 추정은 2가지 경우가 있었다.
1) 중심 극한 정리를 쓰거나 모집단이 정규 분포를 따르는 것을 아는 경우 - 정규 분포를 이용
2) 반드시 모집단이 정규분포여야 해서 정규성 가정이 필요한 경우 - t-분포를 이용
2> 구간 추정 (평균, 분산)

- 추정값이 점 추정을 의미하고
- 정규성 가정을 해야 하므로 t-분포를 이용한 구간 추정이다.
- 신뢰 한계가 구간 추정을 의미한다.
- 분산 추정은 카이-제곱 분포를 이용한 구간 추정이다.
5. 모평균과 모분산에 대한 점 추정, 구간 추정 2 (MEANS)
원래 PROC MEANS는 default로 개수, 최대, 최소, 평균, 표준편차를 필수적으로 알려줌
이 설정이 필요하지 않으면 내가 직접 필요한 통계량을 설정할 수 있었다.
0) CLM
1> CLM = confidence limit mean
2> 여기서 유의 수준(α, ALPHA)을 설정해야 한다.
1) 문법
1> 추가된 것
- PROC MEANS data=SAS-dataset [default 혹은 필요한 통계량] clm alpha=유의 수준(α);
2) 예시
1> 점 추정 & 2> 구간 추정 (평균)

- 표준편차나 분산에 대한 신뢰구간을 같이 구하지는 않는다.
6. 모비율에 대한 점 추정, 구간 추정 (FREQ)
모비율은 베르누이에서 추출한 확률 표본이어서 (정규 분포가 아니어서) t-분포를 이용한 구간 추정이 불가능하다.
0) FREQ에서 중요한 것
읽어들인 자료가 정리된 자료인지 아닌지가 중요
정리되지 않은 자료 : 1 y 2 n 3 y ...
정리된 자료 : y 30 n 100 => 개수를 세라고 하지말고 -> 정리된 숫자 30과 100을 weight로 표시한다.
1) 문법
1> 기존과 유사하며 alpha 옵션을 '/' 뒤에 설정한다.
2) 예시

1> FREQ 기본 문법
- order 설정 : order상 먼저 나오는 값을 기준으로 모비율 추정한다. (ex> yes가 먼저 나오면 yes 비율에 대한 추정한다.)
- default는 알파벳 순서대로 결과를 출력 (=> 그러면 NO에 대한 비율을 추정한다.)
- 'order=data' 설정시 data 상에서 먼저 등장한 순서대로 결과를 추측 (=> YES에 대한 비율을 추정한다.)
- weight count : 정리가 된 자료이고 count를 기준으로 세야하기 때문에 weight를 count로 설정
- exact binomial : 정확히 신뢰 구간을 구할 수 있도록 설정 (이게 없으면 신뢰 구간을 근사로 구하기 때문에)
2> 결과

- ASE : Asymptotic Standard Error
(이전에 모평균 추정에서는 standard error로 s/√n을 설정
=> 여기서 ASE = √[(1-p^)(p^)/n]
- 신뢰 하한 ~ 신뢰 상한이 신뢰 구간을 의미한다. (근사값)
- 정확 신뢰 한계 : 정말로 이항비로 신뢰 구간을 구한다 => 정확한 신뢰 구간을 구할 수 있다.
- 그 뒤에 나오는 검정에 대한 내용은 다음에 다룹니다.
'SAS' 카테고리의 다른 글
| [통계 개념&SAS] 8-1강 - 가설 검정 (단일 표본) (0) | 2020.05.07 |
|---|---|
| [통계 개념] 7-5강 - 모집단이 2개인 경우 통계량 차에 대한 구간 추정 (신뢰 구간) (0) | 2020.05.07 |
| [통계 개념] 7-3강 - 구간 추정 : 신뢰 구간 (0) | 2020.05.07 |
| [통계 개념] 7-2강 - 점 추정 (Point estimation) (0) | 2020.05.06 |
| [통계 개념] 7-1강 - 표본들의 분포 - 카이-제곱 분포, t-분포, F-분포 (0) | 2020.05.05 |



