4. 유의 확률 (p-value)
유의 수준이 작은 것도 중요하지만 기각하는 것이 더 중요하다.
이전에는 주어진 유의 수준에서 기각할 수 있는지만 확인했다.
이번에는 유의 수준을 고정시키지 말고 유의 수준을 얼마까지 높이면 기각할 수 있는지 알아본다.
1) 정의 및 특징
1> 유의 확률 : 귀무가설을 기각할 수 있는 최소한의 확률 (p값, p-value)
2> p보다 크면 기각할 수 있다. => p는 작을수록 좋다.
3> 가설이 다르면 유의 확률도 달라진다.
2) 구하는 방법 (모평균(μ)에 관한 검정 - 모분산(σ)을 모르는 경우) (t분포로 설명)
[우측 검정]
1> 검정 통계량 t0를 구한다.

2> α(확률, 면적)가 t0(x축)을 포함해야 한다. (H1 : 우리가 추정한 T > μ0) → P[T > t0] = p0 (x축인 t0를 확률로 변환)
3> α >= (P[T > t0] = p0) → H0를 기각한다.
4> p-value = P[T > t0]
[좌측 검정과 우측 검정]

※ 하지만 TTEST는 양측 검정의 p-value만 계산한다.

3) 양측 검정의 유의확률을 이용하여 단측 검정의 유의확률 찾는 방법 (SAS를 사용하고 있다고 가정)
1> 현재 상태

- SAS를 통해 양측 검정의 유의 확률 p0를 알고 있다.
1> 우측 검정
먼저 t0(t-value)를 먼저 찾고 음수인지 양수인지 확인한다.
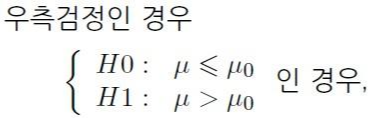
[t0 > 0 인 경우]
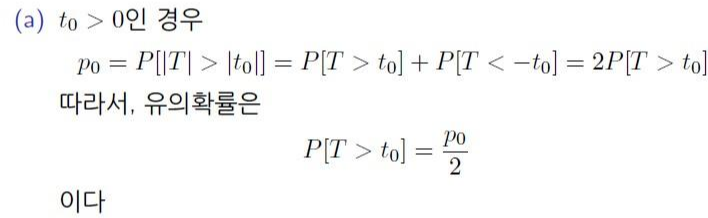
- x축 상의 -t0와 t0의 위치 : ---- -t0 ---- 0 ---- t0 ----
- p0는 검정 통계량의 양 끝 부분의 확률이다. → p0의 절반이 검정 통계량의 우측 부분 확률이다.
- 유의 확률 = p0/2
[t0 < 0 인 경우]


- x축 상의 -t0와 t0의 위치 : ---- t0 ---- 0 ---- -t0 ----
- 유의 확률 = 1 - p0/2
2> 좌측 검정
먼저 t0(t-value)를 먼저 찾고 음수인지 양수인지 확인한다.

[t0 > 0 인 경우]

[t0 < 0 인 경우]

검정에는 가설 설정과 결과가 반드시 있어야 합니다.
가설 설정과 SAS 코딩 후 그 결과를 이용하여
유의 수준을 어떻게 잡으면 귀무 가설을 기각할 수 있는지
아니면 어떤 유의 수준으로도 기각할 수 없는지를 설명하여 같이 제출하세요.
'SAS' 카테고리의 다른 글
| [통계 개념&SAS] 8-4강 - 가설 검정 (독립이 아닌 모집단이 2개인 경우) (0) | 2020.05.12 |
|---|---|
| [통계 개념&SAS] 8-3강 - 가설 검정 (독립인 모집단이 2개인 경우) (0) | 2020.05.12 |
| [통계 개념&SAS] 8-1강 - 가설 검정 (단일 표본) (0) | 2020.05.07 |
| [통계 개념] 7-5강 - 모집단이 2개인 경우 통계량 차에 대한 구간 추정 (신뢰 구간) (0) | 2020.05.07 |
| [SAS] 7-4강 - 점 추정, 구간 추정 실습 (0) | 2020.05.07 |



