모집단이 1개인 경우만 지금까지 배웠고
모집단이 2개인 경우를 이번에 다룰 것입니다.
7. 모집단이 2개인 경우 구간 추정
0) 모집단이 2개인 경우

1> 첫 번째 모집단으로부터 뽑은 확률 표본 X_1, X_2, ... / 두 번째 모집단으로부터 뽑은 확률 표본 Y_1, Y_2, ...
2> 2가지 경우가 있다.
- [1] 처음부터 나뉘어진 두 집단을 비교할 수 있고 (확실히 독립이다.)
- [2] 동일 집단을 시간차에 따라 비교할 수 있다. (독립이 아니다.)
3> 기본 가정이 'X_1 ~ X_m, Y_1 ~ Y_n가 서로 독립'이다.
- 확률 표본의 정의에 의해 X_1 ~ X_m은 iid (서로 독립이고 같은 분포에서 추출), Y_1 ~ Y_n은 iid
- 그러면 X와 Y를 섞어서도 독립이어야 한다.
- [1]번 예시만 해당한다.
1) 두 모평균 차의 신뢰 구간
0> 총 3가지 경우가 있다.
- σ_1^2, σ_2^2을 아는 경우 (정규 분포 사용)
- σ_1^2, σ_2^2을 모름 & σ_1^2 == σ_2^2
- σ_1^2, σ_2^2을 모름 & σ_1^2 != σ_2^2
1> 각각의 모분산을 아는 경우

- 분포와 상관 없이 n만 충분히 크다면 표본 평균은 정규 분포를 따른다.

- 각 표본 평균이 정규 분포를 따르기 때문에 표본 평균의 차 또한 정규 분포를 따른다.
- 이를 표준화하면 Z가 위와 같은 꼴을 가진다.

- 두 집단의 모평균 차에 대한 신뢰 구간을 구할 수 있다.
※ 분산(σ)을 아는 경우가 드물기 때문에 이 경우는 잘 쓰이지 않는다.
cf> 뒤의 2번째 경우에서 달라지는 점
1) 두 모집단이 정규 분포를 따른다. (정규성 가정을 했다.)
2) 두 집단의 분산(σ)이 같다.
2> 각각의 모분산을 모르고 같은 경우
t-분포는 표준 정규 분포와 카이-제곱 분포를 가져와야 했다.
그래서 카이-제곱 분포 1개와 표준 정규 분포 1개를 만든다.
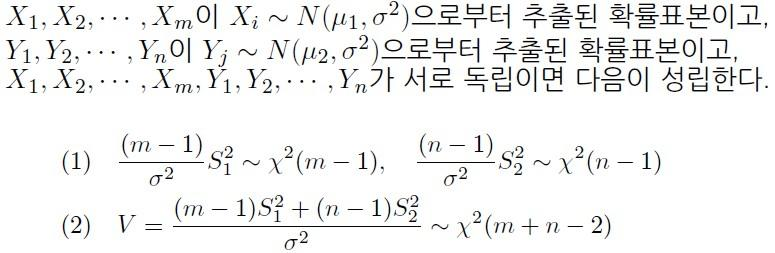
- 각 분포로부터 카이-제곱 분포를 만들 수 있다.
- 그리고 독립된 표준 정규 분포들의 제곱의 합 -> 더하면 여전히 카이-제곱 분포이다.
- 이 때, 모분산(σ)이 같았기 때문에 계산을 깔끔하게 할 수 있다.
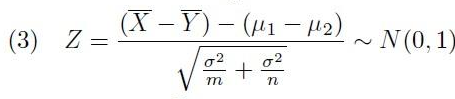
- 각각의 표본 평균이 정규분포를 가지니까 이들의 차를 표준화 한 것은 표준 정규 분포를 가진다.
(표본 평균의 분산은 각각의 표본 평균의 분산을 더한 것이 된다.

- 그러면 기존 표준 정규 분포 변수의 분모인 모분산 부분을 표본 분산으로 대체한다.
(이 표본 분산 자리에 '표본합동분산' 개념을 사용한다.)
- 이처럼 t-분포를 만들 수 있다.

cf> 표본합동분산
1) 모분산에 대한 불편추정량이다.
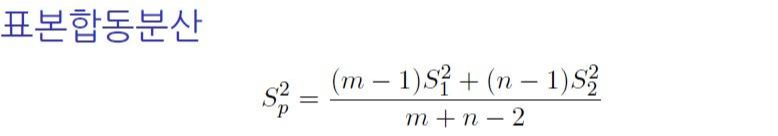
2) s_2^2은 σ_2^2의 불편 추정량, s_1^2은 σ_1^2의 불편 추정량
3) 하지만 이들이 같은 상황이므로 이들의 가중 평균으로 분산을 계산한다.
3> 각각의 모분산을 모르고 다른 경우

2) 두 모분산 비의 신뢰구간
1> 조건
- 모두 정규 분포에서 추출된 확률 표본(X_1~X_m, Y_1~Y_n)이다.
- X_1, ..., X_m, Y_1, ..., Y_n은 서로 독립

2> 신뢰 구간

'SAS' 카테고리의 다른 글
| [통계 개념&SAS] 8-2강 - 유의 확률 (p-value) (0) | 2020.05.07 |
|---|---|
| [통계 개념&SAS] 8-1강 - 가설 검정 (단일 표본) (0) | 2020.05.07 |
| [SAS] 7-4강 - 점 추정, 구간 추정 실습 (0) | 2020.05.07 |
| [통계 개념] 7-3강 - 구간 추정 : 신뢰 구간 (0) | 2020.05.07 |
| [통계 개념] 7-2강 - 점 추정 (Point estimation) (0) | 2020.05.06 |



