3. 구간 추정 (Interval Estimation)
1) 신뢰 구간 (Confidence Interval)
1> 정의

- 모수 θ가 L(X)와 U(X) 사이에 있을 확률 = 1-α
- (L(X), U(X)) = 모수 θ에 대한 신뢰 수준 1-α (신뢰도 100*(1-α)%)인 신뢰구간
2> 신뢰 구간을 구하기 위해 해야할 것
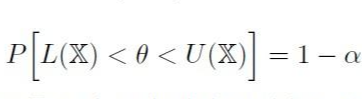
그럼 θ가 어떤 구간에 들어갈 확률을 구해야 한다.
이를 알려면 어떤 분포인지 알아야 한다.
[1] θ의 범위에 대한 확률을 알려면 θ가 분포에 포함되어야 한다.
L(X)와 U(X)가 통계량이어야 하므로 L(X)와 U(X)에는 표본에 관련된 식만 있어야 한다.
[2] 분포에 θ이외의 모수는 포함하지 않아야 한다.
3> (앞에서 배운) μ를 포함하는 분포 1 - 정규 분포
- 정규 분포
(n이 충분이 크다면) 중심 극한 정리에서 표본 평균을 표준화 한 것이 표준 정규 분포를 따르는데 μ를 포함한다.
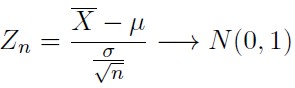
X가 그냥 정규 분포를 따른다면 μ를 포함한다.
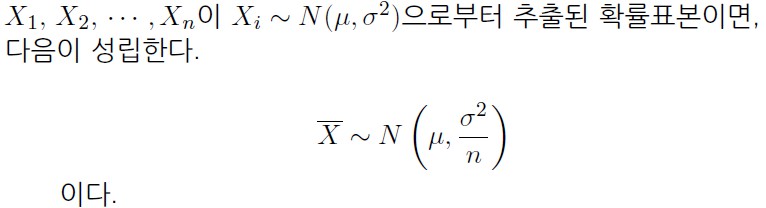
장점 : 어떤 분포든 상관 없이 표본의 크기만 크면 사용할 수 있다.
단점 : σ를 제거해줘야 한다. (σ를 이미 알고 있어야 한다.)
4> (앞에서 배운) μ를 포함하는 분포 2 - t-분포
- t-분포

단점 : 반드시 정규 분포에서 추출한 표본이어야 한다.
장점 : 표본 분산이 필요하므로 위의 경우와 달리 σ를 몰라도 이 분포를 사용할 수 있다.
2) μ의 신뢰 구간
1> σ^2이 알려진 경우 (위에서 정규 분포 case)
[1] n이 충분이 크거나(중심 극한 정리) or [2] 그냥 모집단이 정규 분포를 따르거나

cf> Z_α

α는 상위 확률이다.
t-분포, 카이-제곱 분포, F-분포에도 이와 같은 개념이 있다.
2> σ^2을 모르는 경우 (위에서 t-분포 case)
반드시 모집단이 정규분포이어야 한다. (반드시 정규성 가정이 필요)

- s와 t_α/2(n-1)만 변경되었다.
3) σ^2의 신뢰구간
찾자
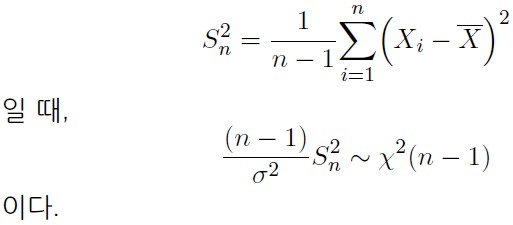
1> σ^2의 신뢰구간

cf> 추정의 표준오차
α가 작을 수록 (신뢰 수준 1-α가 높을 수록) -> Z_α가 커진다. -> 신뢰 구간이 넓어진다.
α 말고도 σ/√n에 따라 신뢰 구간이 바뀌므로
σ/√n or s/√n= 추정량의 표준편차 = 표준오차
로 정의한다.
단순하게 신뢰 구간 반쪽에서 분포가 차지하는 부분을 제외한 부분이다.
4) 모비율의 신뢰 구간
1> 표본 비율
- X_i ~ Ber(p)

2> 비율에서의 중심 극한 정리

3> 모비율의 신뢰 구간
- 명백하게 X가 베르누이 분포를 따르므로 (정규 분포를 따르지 않으므로 t-분포를 사용할 수 없다.)
=> 정규 분포 가정이 필요한 case (σ^2 모르고 t-분포 사용하는 case)를 쓸 수 없다.
=> 그래서 무조건 n이 충분하다는 전제가 필요하다. (np >= 5, n(1-p) >= 5)
=> 만약 괄호의 조건을 만족하지 않으면 SAS에서 경고 메시지를 준다. (조건을 만족하지 않으니 정확하지 않을 수 있다고)
- 중심 극한 정리에 따라 p^ ~ N(p, pq/n)
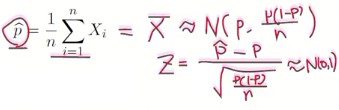
- 그런데 Z 내부에 p가 너무 식 안에 많다
=> 분자의 p는 평균에 해당되지만
=> 분모는 표준편차에 해당되므로 => 분모 부분만 p 대신에 p^으로 대체해서 신뢰구간을 구한다.

cf>
1> σ를 아는 경우 => 정규 분포 이용
[1] n이 일정 이상 크거나 [2] 정규 분포를 따를 때
=> 정규 분포 사용
2> σ를 모르는 경우
=> 무조건 정규 분포를 따르고 있어야 한다. (따르지 않으면 가정을 하는 경우도 있습니다.)
=> t-분포 사용
'SAS' 카테고리의 다른 글
| [통계 개념] 7-5강 - 모집단이 2개인 경우 통계량 차에 대한 구간 추정 (신뢰 구간) (0) | 2020.05.07 |
|---|---|
| [SAS] 7-4강 - 점 추정, 구간 추정 실습 (0) | 2020.05.07 |
| [통계 개념] 7-2강 - 점 추정 (Point estimation) (0) | 2020.05.06 |
| [통계 개념] 7-1강 - 표본들의 분포 - 카이-제곱 분포, t-분포, F-분포 (0) | 2020.05.05 |
| 6-3강 - 자료의 정리 및 요약 3 (FREQ) (0) | 2020.04.26 |



