2. 점추정
1) 통계량과 불편추정량
1> 통계량 (statistic)
[1] θ를 포함하지 않는 [2] 표본 X_i 들에 대한 함수를 통계량으로 부른다.
- θ가 모수이고 θ를 추정해야 하는데 θ를 포함하면 이 함수(통계량)로 θ를 추정할 수 없다.
- 추출한 각 표본 X_i에 대해 벡터 표현을 사용 (X = (X_1, X_2, ... , X_n))

2> 점 추정의 의미
이렇게 정의한 통계량들 중에서 하나로 점 추정을 할 건데
점 추정 = point estimation = '한 점' = '통계량 하나로 추정한다.' 라는 의미로 확장된다.
cf> 점 추정과 구간 추정의 장단점
1> 점 추정의 장점 : 추정 결과를 보는 사람이 받아들이기 쉽다.
2> 점 추정의 단점 : 추정하는 사람은 하나로 추정하다보니 틀릴 수 있다.
3> 그래서 점 추정은 기준을 정하고 기준에 따라 추정한다. (기준에 따라 불편 추정량, 일치 추정량, 최우 추정량)
4> 구간 추정의 장점 : 추정하는 사람이 잘 예측할 수 있다.
5> 구간 추정의 단점 : 구간을 무작정 길게 잡으면 맞출 확률은 높으나 추정 결과를 보는 사람이 받아들이기 어렵다.
6> 그래서 구간 추정은 신뢰 수준을 제시한다.
3> 불편 추정량을 사용하는 이유
- 평균이 같다고 같은 분포는 아니지만
- 최소한 통계량의 기댓값과 추정하고자 하는 모집단의 기댓값을 같게 해보자는 것이 불편 추정량
4> 불편 추정량 (Unbiased Statistic)

2) 표본 평균, 표본 분산
1> 정의

- 이들도 하나의 분포를 이룬다.
- 이들의 분포를 알려면 X가 무슨 분포인지 알아야 한다. (하지만 X에 대해 추정하는 것이므로 X가 무슨 분포인지 모를 수 있다.)
- 그래서 X가 무슨 분포인지 알려주는지 확인한다.
2> Theorem

(모평균이나 모분산을 알 수도 있고 모를 수도 있다.)
- 위의 사실과 관계없이 표본 평균과 모평균이, 표본 분산과 모분산이 이와 같은 관계를 가진다는데 의의가 있다.
(현재 평균과 분산이 있다는 것만 알지 분포는 모른다.)
- 그리고 꼭 X가 정규 분포가 아니어도 (어떤 분포인지 몰라도) 이 Theorem이 성립한다.
그런데 어떤 분포에 근사하는지 정도는 알 수 있다.
3) 중심 극한 정리
1> 중심 극한 정리

(확률 표본이 있는데 어떤 분포인지 모르니 어떤 분포이든 상관없이)
- 표본 평균이 μ, 표본 분산이 σ^2이기만 하면
- 표본 평균이 위와 같은 정규 분포로 근사한다.
2> Theorem
- 아래 정리로 불편 추정량을 찾을 수 있다.

표본 평균은 모평균의 불편추정량이고, 표본 분산은 모분산의 불편추정량이다.
(표본 표준편차가 모표준편차의 불편추정량은 아니지만 그냥 표본 표준편차로 사용한다.)
- 그렇다면 우리는 SAS에서 표본의 평균과 분산을 찾아야 한다.
=> 이를 PROC의 univariate, mean, summary로 구할 수 있다.
이제 표본의 분포를 찾는 것이 목적이다.
하지만 모집단의 분포를 모르니 찾기가 어렵다.
일단 모집단의 분포를 가장 많이 쓰이는 분포로 가정한다.
그래서 먼저 정규 분포라는 전제 하에 표본의 분포를 찾는다.
3> 표본 평균과 표본 평균의 분포 (정규 분포와 카이-제곱 분포)
중심 극한 정리 : 모집단이 정규분포가 아니여도 표본 평균이 정규 분포로 근사한다.
(표본 평균의 평균 ~ μ | 표본 평균의 분산 ~ σ^2)
이번 정리 : 모집단이 정규분포이면 표본 평균이 정규 분포이고 표본 분산은 일정 수를 곱하면 chi-square 분포이다.)
(표본 평균은 '표본 평균의 평균 = μ | 표본 평균의 분산 = σ^2' 인 정규분포를 가진다.)
(표본 분산은 n-1/σ^2를 곱하면 자유도 n-1인 chi-squre 분포를 가진다.)

4> 표본 평균의 분포 (t-분포)
- 7-1강에서 자유도 n인 t-분포 만들 때
- 분자 : 표준 정규 분포 따르는 것을 분자에
- 분모 : 카이-제곱 분포 따르는 것을 n으로 나누고 루트 씌운 것을 분모로
- 대입을 통해 아래 식이 t-분포를 따르는 것을 확인할 수 있다.
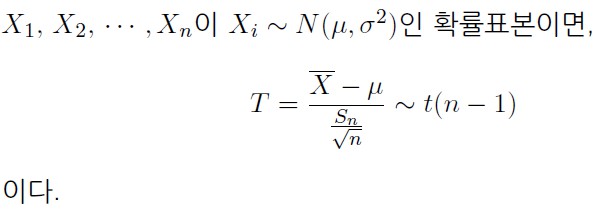
- T의 값이 중심 극한 정리에서 표본 평균을 표준화한 것과 분산만 다르고 나머지는 같다. (T는 표본 분산을 사용한다.)
결론
1) 점 추정은 SAS로 쉽게 구현할 수 있다.
2) 기술 통계량만 출력하면 되기 때문이다.
=> 이를 PROC의 univariate, mean, summary로 구할 수 있다.
'SAS' 카테고리의 다른 글
| [SAS] 7-4강 - 점 추정, 구간 추정 실습 (0) | 2020.05.07 |
|---|---|
| [통계 개념] 7-3강 - 구간 추정 : 신뢰 구간 (0) | 2020.05.07 |
| [통계 개념] 7-1강 - 표본들의 분포 - 카이-제곱 분포, t-분포, F-분포 (0) | 2020.05.05 |
| 6-3강 - 자료의 정리 및 요약 3 (FREQ) (0) | 2020.04.26 |
| 6-2강 - 자료의 정리 및 요약 2 (BOXPLOT, SUMMARY) (0) | 2020.04.26 |



