0. Background
순차회로의 경우 이전의 combinational system과 달리 history까지 고려해서 다음 state를 결정합니다. 그로 인해 Truth Table 만으로는 값의 변화를 효율적으로 나타내기 어려울 수 있습니다. 그래서 순차회로를 더 잘 표현할 수 있도록 State Diagram과 State Table을 사용합니다.
1) State Table
Truth Table에서는 어떤 input들이 주어졌을 때, output이 어떤 state를 가지는지만 파악했다면
State Table은 순차회로 특성에 맞게 input과 history를 동시에 고려합니다. State Table은 위의 가로줄은 input 조합, 왼쪽 세로줄은 history(현재 상태)가 주어지고 '이 history(현재 상태)를 가진다면 특정 input 조합이 주어지면 다음에는 state가 어떻게 변할지' 알려줍니다.

예를 들어, 지금 state table의 경우 왼쪽에는 과거 A, B의 state 경우의 수가 있고, 위의 가로줄은 input이 X가 0 또는 1일 때를 보여주고 있습니다. 이처럼 input과 history를 동시에 고려해서 남은 빈칸(다음 state)을 채워넣습니다.
2) State Diagram

State Diagram또한 State Table과 동일하게 input과 history를 동시에 고려하여 다음 state를 알려줍니다.
위의 그림에서 동그란 부분이 현재 state이며, 화살표에 적힌 왼쪽 숫자가 input으로 이 input을 받았을 때의 output이 바로 input 옆의 숫자입니다. 그리고 그 화살표가 가리키는 곳의 값이 바로 다음 state의 값입니다.
1. Finite State Machine
순차 회로를 만드는 수학적/이론적 model
cf> Finite State Machine
바로 번역을 하면 '한정된' '상태'를 연산하는 '기계'정도로 볼 수 있습니다. 이 기계는 한정된 state를 가지는데, 이 기계는 어떤 사건에 의해 state를 바꿔가는 기계입니다. 그래서 Finite State Machine도 순차회로의 종류입니다. (그래서 이전 시간에 다룬 Flip-Flop과 Latch처럼 익숙할 것입니다.) 이 Finite State Machine은 크게 Moore Machine과 Mealy Machine으로 나뉩니다.
1) 구성
1> I : input combination 집합
2> O : output combination 집합
3> S : state 집합
2) function
1> f(I, S) : next state function
2> g : output function
- Moore Model : g(S)
- Mealy Model : g(I, S)
3) Moore Model
현재 state로 다음 state를 결정합니다. (그래도 현재 input이 다음 state 결정에 영향을 미칩니다.)
0> Mealy Machine과 달리 state의 개수는 sequence 길이보다 1개 더 많아야 합니다.
1> (state diagram) 그래서 state에 output을 표기합니다. (state가 곧 output입니다.)

2> (state table) 현재 input과 관계 없이 현재 state만으로 output이 같기 때문에
현재 input(x)을 구분하지 않고 output을 그냥 표기합니다.
4) Mealy Model
현재 state와 현재 input을 통해 다음 state를 결정합니다.
1> (state diagram) 그래서 arc(화살표)에 현재 input을 표기합니다.

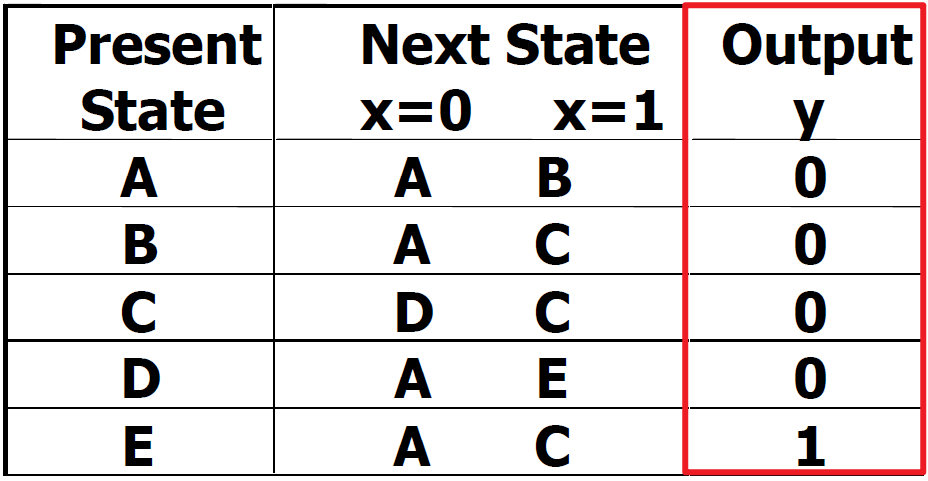
2> (state table) 현재 input에 따라 output은 다르기 때문에 현재 input(x)에 따라 output을 따로 표기합니다.

2. Moore Machine
1) 특징
1> 현재 input을 제외하고 그 이전의 input pattern(현재 state)을 가지고 output을 결정합니다.
2> 현재 input 이전의 input들을 고려하기 때문에 첫번째 output은 알 수 없습니다.
2) 예시
연속적으로 1이 3번 나와야 output으로 1을 출력하는 구조입니다.

언급했던 특징대로 현재 input이 0이더라도 과거에 1이 연속적으로 3번 나왔다면 1을 출력합니다.
1> State Table

현재의 input과 상관없이 output 값을 가지는 것을 state table에서 확인할 수 있습니다.
다만 현재의 state는 고려합니다. 그런데 현재 state는 과거 시점의 input에서 비롯된 것입니다. 그래서 과거 input의 pattern이 output과 state 변화에 영향을 미칩니다.
2> State Diagram

연속적으로 input이 1이 나와서 D까지 도달하기만 하면 output이 1인 나온다. (D에 도달하고 나서야 1을 출력하므로 여기서 아래 Mealy Machine과 달리 delay이 생깁니다.)
3. Mealy Machine
1) 특징
1> 현재 input은 물론하고 현재 state를 가지고 output을 결정합니다.
2) 예시
이번에도 연속적으로 1이 3번 나와야 output으로 1을 출력하는 구조입니다.

다만 이전 Moore Machine과 달리 현재의 input까지도 input pattern으로 고려하여 이를 output 출력에 반영합니다.
그래서 이전에는 1번의 delay이 있던 것과 달리 input이 조건을 만족하는 그 즉시 1을 출력합니다.
1> State Table

이전과 달리 input에 따라 output 값이 다를 수 있습니다.
2> State Diagram

이전 Moore Machine과 달리 C에서 input을 1로 받으면 output을 1로 출력할 수 있다. 그래서 delay가 발생하지 않습니다.
cf> Finite State Machine Example
101이 나오면 output이 1로 바뀌는 Finite State Machine

example을 보면 101을 입력한 직후에 output이 1을 출력합니다.
이는 현재 state(과거 맥락)과 현재 input을 모두 고려하기 때문에
Mealy Machine입니다.
1) State Graph
101이 기준이니 총 state는 3개입니다.

2) State assignment
1> 필요한 Flip-Flop의 개수 설정

binary number로 state 3개를 나타낼 수 있으려면
binary number가 2개 필요합니다. (2개의 binary number로 4개의 state를 표현할 수 있습니다.)
=> 즉, 3개의 state를 표현하는데 Flip-Flop이 2개 있으면 됩니다.
2> state assignment 할당
S0 : 00
S1 : 01
S2 : 10
그리고 앞자리 수는 T Flip-Flop으로, 뒷자리 수는 SR Flip-Flop으로 설정합니다.
(문제에서 T Flip-Flop과 SR Flip-Flop으로 만드라고 되어있습니다.)
3> state table을 기반으로 excitation table 만들기

(excitation table : 특정 current state에서 특정 next state가 되기 위한 input이 조합)
각 Flip-Flop들의 excitation table은 외워두는 게 좋습니다.

3) State Table [Flip-Flop 관점]
A : 앞자리 수 current state (A*가 next state)
B : 뒷자리 수 current state (B*가 next state)
x : input
z : output
TA : T Flip-Flop(A)의 T
SB : SR Flip-Flop(B)의 S
RB : SR Flip-Flop(B)의 R

4) Karnaugh Map
1> z (output)

2> TA, SB, RB

5) Circuit
(기존 Flip-Flop의 구조를 알야야 합니다.)
1> Flip-Flop들 먼저 그립니다.
2> Flip-Flop의 input들을 그립니다. (state와 input들로 만든 K-map 기반으로)


문제의 경우의 수
1> Moore로 접근 vs Mealy로 접근
2> 어떤 위치에 어떤 flip-flop을 사용하는지
'디지털 회로 개론' 카테고리의 다른 글
| 6-3강 - Sequential Circuit Design 3 (Parity Checker example) (1) | 2020.12.02 |
|---|---|
| 6-2강 - Sequential Circuit Design 2 (Sequence Detector example - Mealy & Moore) (0) | 2020.12.01 |
| 5-2강 - Analysis of Sequential Systems 2 (Flip Flops) (0) | 2020.11.13 |
| 5-1강 - Analysis of Sequential Systems 1 (Latch) (0) | 2020.11.13 |
| 4-4강 - Combinational System Design 4 (ROM, PLA, PAL) (0) | 2020.10.23 |



