6. Counter Example
0) Synchronous Counter
0> Example
2-bit Counter이며
x=1일 때에만, binary state가 00, 01, 10, 11로 변하고
x=0일 때에는 회로가 변하지 않는다.
1> State Diagram

2> State Table

3> JK Flip-Flop 관점으로 만든 State Table
[1] JK Flip-Flop Exciation Table
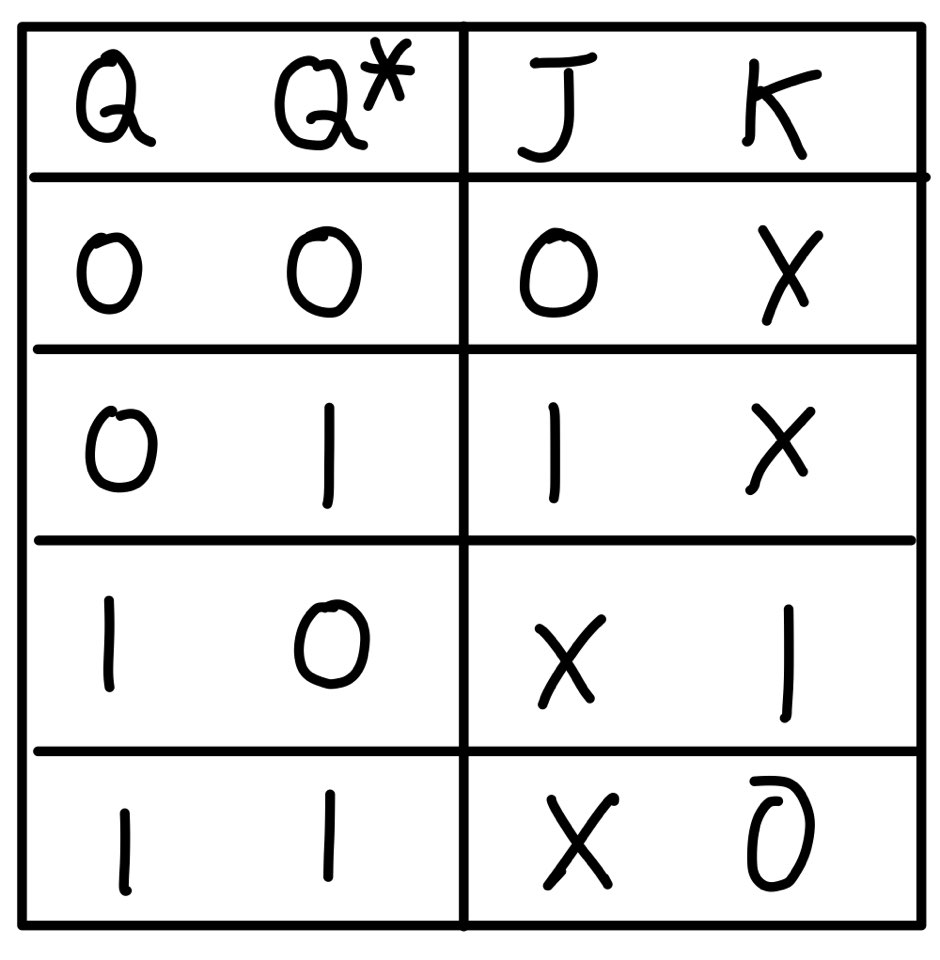
[2] JK Flip-Flop 관점으로 만든 State Table

4> Karnaugh Map

1) 2-bit Countdown Counter
※ 특이한 점 : output이 없다. state가 이미 binary number이다.
0> 문제 소개
x=0일 때는 변화가 없고
x=1일 때는 11 -> 10 -> 01 -> 00 -> 11 -> ... 과 같은 변화가 있습니다.
counter이기 때문에 output이 따로 존재하지 않고 state가 곧 output입니다. (input이 없을 수도 있습니다.)
1> State Diagram
[1] state 정의
11, 10, 01, 00은 각각 3, 2, 1, 0을 의미합니다.
[2] [3]

2> State Table
[1] (col) present state, next state
[2] (row) state 모두 적기
[3] 빈칸 채우기

[4] state assignment
현재 총 4개의 state가 있기 때문에 Flip-Flop이 2개 필요합니다.
이 때, A와 B라는 2개의 JK Flip-Flop을 준비합니다.
그로 인해 JA, KA는 A의 2개 input을 의미하고, JB, KB는 B의 2개 input을 의미합니다.
3> excitation table
[1] JK Flip-Flop excitation table

[2] State Table

4> Karnaugh map
(생략)
5> 회로도
(생략)
2) input이 2개
※ 특이한 점 : input이 2개이다.
0> 문제 소개
state 0에서 input (x, y)이 (1, 1)일 때만 state 1로 변합니다.
state 1에서 input (x, y)이 (0, 0)일 때만 state 0으로 변합니다.
1> state diagram
[1] state 정의
1과 0이라는 2개의 state가 존재합니다. (고로 1개의 flip-flop만 있으면 됩니다.)
[2] [3]

3) Binary Counter
0> Ripple Counter & Synchronous Counter
4) Binary Counter with parallel load
0> 개념 설명

[1] register는 여러 Flip-Flop으로 구성되어 있습니다. 그래서 data를 저장하는 기능을 합니다.
[2] load : clock pulse를 막거나 발생시킵니다.
- load=0이면 clock pulse를 막아서 input data가 register(4-bit D Flip-Flop)로 load되지 않습니다.
- load=1이면 clock pulse를 활성화해서 input data가 register로 load하고 그에 따라 output을 만듭니다.
[3] inc (increment) : counter를 증가시킵니다. (질문 : inc가 1이고 load도 1인 경우?)
- inc = 1이면 counter의 값이 다음 값으로 증가합니다.

5) Irregular Counter
숫자가 증가하는 방향으로 count하는 것이 아니라
특정 순서대로 숫자가 바뀌는 counter입니다.
0> 문제 소개
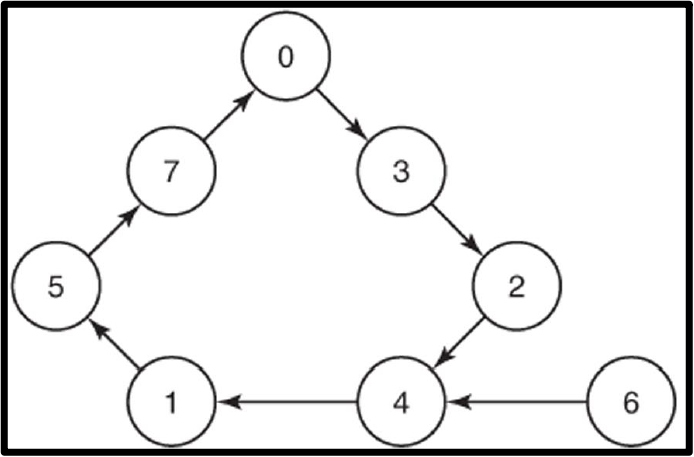
예를 들어, 0, 3, 2, 4, 1, 5, 7, 0, 3, 2, 4, ... 과 같이 숫자가 일정 주기로 변할 수 있습니다.
(※ 이 때, 6이 포함되지 않았음을 인지합니다.)
그리고 input, output은 없다고 가정합니다.
<state assignment>
0~7을 표현하기 위해서는 3개의 flip-flop이 필요합니다.
이 때, q1, q2, q3를 각각 D flip-flop의 output으로 정의합니다.
1> State Diagram
Counting에 포함되지 않은 state가 있어서 State Diagram은 마지막에 그립니다.
2> State Table

중요한 것은 6이 counting에 없더라도
[1] state table에 표기하고
[2] next state를 don't care로 표기해야합니다.
3> Excitation table
[1] D Flip-Flop
[2] State Table
4> Karnaugh map

1> State Diagram (State 6 ???)
counting에 포함되지 않은 state도
위의 Karnaugh map을 기반으로 next state를 구합니다.
[1] present flip-flop output
present state 6 : (q1, q2, q3) = (1, 1, 0)
[2] present flip-flop input
D1, D2, D3 구하기

[3] next flip-flop output
q1* = D1
q2* = D2
q3* = D3
(이기 때문에 그냥 D1, D2, D3만 구해도 됐었습니다.)
(q1*, q2*, q3*) = (1, 0, 0)
그러므로 6의 next state는 처음에 don't care로 설정했지만 회로를 완성하니 next state는 4가 됩니다.