모비율 뿐 아니라 모평균 차도 3개 집단이 넘어가면 어떻게 할까? 분산분석으로 해결
1. 일원 배치법
0) intro
실험에서 가장 중요한 요인이 무엇인지 알고 있는데 실제로 그러한지 알고 싶다.
1> 파악하고자 하는 것
- 이 요인이 가장 중요한 요소인가?
- 그렇다면 이 요인이 어떤 수치일 때 가장 효과적인가? (최적화)
1) 기본
0> 정의 : 어떤 실험의 결과가 한 요인에 의해서 결정된다고 가정하에 다른 가정은 동일하게 유지하고 그 요인의 수준만 달리 하여 실험하는 방법을 일원 배치법이라 한다.
1> 자료구조

- 요인 수준 : 해당 요인을 다 다르게 설정한다.
- 실험의 반복 : (한 번만 실행하면 정확도가 떨어지니) 여러번 실행한 결과를 기록
x_ij : i번째 요인 수준으로 j번째 실험한 결과
2> 검정하고자 하는 것

(H1 : 하나라도 다른 게 있다.)
- 형태가 모집단이 2개인 경우에 대한 검정과 비슷한데 3개 이상이 되면 단순히 PROC TTEST로 검정할 수 없었기 때문에 지금처럼 분산분석을 시행한다.
(정의 : 어떤 실험의 결과가 한 요인에 의해서 결정된다고 가정하에 다른 가정은 동일하게 유지하고 그 요인의 수준만 달리 하여 실험하는 방법을 일원 배치법이라 한다. => 그래서 수준을 여러가지로 다양하게 하려면 분산분석을 이용해야 한다.)
- 어떤 원리로 진행하는가? (이전에 한 검정에서 hint를 얻는다.)
-> 짝표본 검정이 아니라 독립 이표본에 가깝다.
-> [1] 정규성 가정을 했으며
-> [2] 분산이 같은 경우와 다른 경우로 나누었다.
3> 기본 가정

- 정규성
- 등분산성
- 독립성
4> 오차

각 요인 수준에서 하나의 자료와 그 요인 수준에서 자료들의 평균의 차
5> 주효과 (수준 효과)
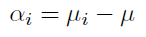
α_i = 0인 것은 H0에서 모든 평균들이 같다는 것과 같다.
6> 모형

- x_ij - μ = (x_ij - μ_i) + (μ_i - μ)
α_i는 수준 별로 차이가 나서 수준 효과라고 부르기도 한다.
ε_ij는 실험할 때마다 차이가 난다. 실험 오차
- 이처럼 오차를 2종류로 분류했다.
각 효과 중 어떤 것이 큰 지도 살펴본다.
- 이제 μ_i를 x˘로 두고 조절해본다.
cf> 분산 분석으로 부르는 이유
분산이 평균에서 얼만큼 떨어져 있는지를 각각의 효과에 대한 편차로 구분해서 분석하려고 함
2) 총 변동의 분할
1> 총 편차

위에서 얘기했듯이 2개로 분할할 수 있다.
하지만 단순히 합하면 0이 나오기 때문에 유용하지 않고 이를 제곱해서 사용한다.
2> 제곱합
x_ij가 N(μ_i, σ^2)를 따름 , 서로 독립, 등분산
ε_ij는 N (0, σ^2)를 따름, 서로 독립, 등분산
- SST (총 제곱합 : Total Sum of square)


=> SST = SSE + SSA
- SSE

- SSA

3> 자유도의 분할
(편차의 합은 0이 되어야 한다. 그래서 n개의 편차가 있으면 n-1개는 자유롭게 정하고 나머지 하나는 자동으로 결정된다.)
Φ_T = nr-1
Φ_E = n(r-1)
Φ_A = n-1
Φ_T = Φ_A + Φ_E
3) 제곱합과 평균제곱
1> 제곱합에 자유도를 나눈값을 평균제곱(Mean Square)라고 한다.

2> 요인 수준별 평균의 분포
(x_ij ~ N(μ_i, σ^2))

3> MSE와 MSA의 기댓값

Φ_A와 r 모두 0보다 크다
-> E[MSA] > E[MSE]
4) 평균 제곱의 분포

위의 분포를 기반으로 표준화한다.


5) 평균 제곱의 분포 - 검정 관점
H0가 사실이라는 전제 하에 분포에 어떤 변화가 생기는지
1>

2>

위의 식을 V라 할 때
3>
F = (V/(n-1)) / (U/n(r-1)) ~ F(n-1, n(r-1))
F = MSA/MSE

이전에 MSA의 값이 MSE보다 컸었다. Φ_A 내부의 α_i가 클수록 차이가 커진다.
=> SSA가 SSE보다 크다.
6) 수준 효과의 존재성에 대한 검정
1> 가설

이 H0는 α_i의 값들이 모두 0이라는 것과 같은 말이다.
α_i 크다 -> H0와 다르다. -> MSA의 값이 MSE보다 크다.
2> 검정 통계량

3> F0 > Fα(n − 1, n(r − 1))

7) 분산분석 표

8) 각 수준에서의 모평균 μ_i 추정

각 수준에서의 모평균 μ_i의 신뢰 구간의 폭은 수준에 관계없이 일정하다.
9) 각 수준에서의 μ_i - μ_j의 추정


이와 같은 모평균에 대한 추정은 처음 분산분석이 기각되고 나서 사용한다. (분산 분석이 기각되지 못하면 할 필요 없다.)
10) 다중 비교
분산 분석이 기각되었을 때, 구체적으로 어떤 수준간의 차이가 나는지 알아보기 위한 방법
1> LSD
관심있는 두 수준의 차에 관한 검정으로 어떤 두 수준을 선택해도 기각될 최소의 차(최소유의차)는
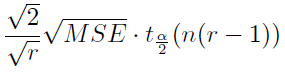
이다.
2> 대비
각 수준의 비가 일정한지 알아 볼 수 있는 t검정이다
3> Bonferroni
개별적인 t 검정에서 각각의 유의수준을 α/m 으로 하여 전체적인 유의수준이 α가 되도록 하는 것으로
실험하기 전에 미리 비교하는 두 평균의 차만 검정할 때 사용
4> Scheffe
대비에서 t값 대신 F값으로 대체하여 신뢰구간을 조정한 것으로 Tukey나 Bonferroni에 비해 보수적임
5> Tukey : 표준화범위를 이용하는 것으로 모든 가능한 두 평균들간의 비교에 유용
6> Duncan : Tukey와 달리 몇 단계로 나누어 다중비교하는 방법으로 Tukey에 비해 비교적 귀무가설을 잘 기각 할 수 있음.
'SAS' 카테고리의 다른 글
| 10-3강 - 이원배치법 (0) | 2020.06.08 |
|---|---|
| 10-2강 - 일원배치법 실습 (0) | 2020.06.08 |
| 9-1강 - 범주형 자료의 분석 (0) | 2020.06.08 |
| [통계 개념&SAS] 8-5강 - 모비율 차에 대한 검정 (0) | 2020.06.08 |
| [통계 개념&SAS] 8-4강 - 가설 검정 (독립이 아닌 모집단이 2개인 경우) (0) | 2020.05.12 |



