일원배치법에서 하나의 요인을 다뤘다면
이원배치법에서는 2개의 요인이 모두 효과가 있는지 확인한다.
요인이 A, B가 있어서
A1, A2, A3
B1, B2, B3
로 3종류씩 있다면 자료를 어떻게 표현할 것인가?
4. 이원 배치법
1) 기본
1> 자료 구조

x_ijk : i번째 A수준, j번째 B수준을 가지는 data 중에서 k번째 data
- x_ijk - μ = (x_ijk - μ_ij) + (μ_i.. - μ) + (μ_.j. - μ) + (μ_ij - μ_i.. - μ_.j. + μ)
(x_ijk - μ_ij) : ε_ijk
(μ_i.. - μ) : A의 효과
(μ_.j. - μ) : B의 효과
(μ_ij - μ_i.. - μ_.j. + μ) : γ_ij (교호 작용)
2> 기본 가정
정규성, 등분산성, 독립성

3> 오차
기본 가정 3가지 적용

4> 주효과

5> 모형

2) 총변동의 분할
1> 총 편차

2> 제곱합

SST = SSA + SSB + SSAB +SSE
3> 자유도의 분할

abr-1 = (a-1) + (b-1) + (a-1)(b-1) + ab(r-1)
4> 분산분석표

3) 이원배치 분산분석의 검정
1> A의 효과에 대한 검정

2> B의 효과에 대한 검정

3> 교호 작용(A와 B가 겹쳐서 생기는 효과)에 대한 검정

5. 이원배치 분산분석 실습
제품이 팔리는 것이 디자인과 도시에 따라 어떤 영향을 미치는지 확인하려고
1) 예제
1> 코드
DATA sales;
DO city = 'Lagre ', 'Middle', 'Small ';
DO design = 'A', 'B', 'C';
DO rep = 1, 2, 3;
INPUT sales @@;
OUTPUT;
END;
END;
END;
CARDS;
23 20 21 22 19 20 19 18 21
22 20 19 24 25 22 20 19 22
18 18 16 21 23 20 20 22 24
;
RUN;
PROC ANOVA DATA=sales;
CLASS city design;
MODEL sales= city design city*design;
MEANS city design city*design;
RUN;
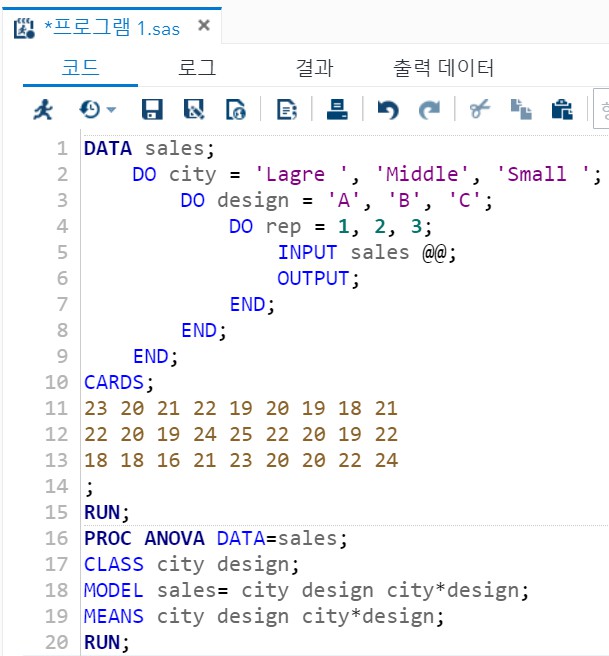
- DO에서 문자열의 개수를 모두 같게 해주어야 한다.
- class로 city와 design이다.
2> 결과 1

- class가 city와 design 2개이며 3종류씩이다.
- Model : Error를 제외한 나머지를 한 번에 본다. (a에 의한, b에 의한, ab에 의한 효과를 합쳐서 본다)
(맨 마지막 표에서 구분해준다.)
기각할 수 있다. 이제 세부적으로 보기 위해 아래로 내려간다.
- 마지막 표
design과 city*design은 기각할 수 있다. 효과가 있다.
3> 결과 2 (MEANS) - city
딱봐도 별 차이 없어보인다.

4> 결과 3 (MEANS) - design
살짝 차이가 난다.

5> 결과 4 (MEANS) - city*design
교호 작용 효과가 크다.

cf> 교호 작용 그림 (정식 버전)
PROC SUMMARY DATA =sales NWAY;
CLASS city design;
VAR sales;
OUTPUT OUT=meanout MEAN (sales) =mean;
RUN;
SYMBOL1 I=JOIN W=1 V=DOT CV=BLACK H=2;
SYMBOL2 I=JOIN W=1 V=CIRCLE CV=RED H=2;
SYMBOL3 I=JOIN W=1 V=SQUARE CV=BLUE H=2;
PROC GPLOT DATA=meanout;
PLOT mean*city=design;
RUN;'SAS' 카테고리의 다른 글
| [SAS] 11-2강 - 단순 선형 회귀 분석 실습 (0) | 2020.06.09 |
|---|---|
| [통계 개념] 11-1강 - 단순 선형 회귀 분석 (1) | 2020.06.08 |
| 10-2강 - 일원배치법 실습 (0) | 2020.06.08 |
| 10-1강 - 일원 배치법 (0) | 2020.06.08 |
| 9-1강 - 범주형 자료의 분석 (0) | 2020.06.08 |



