<Intro>
1) 모비율 차에 대한 검정도 모평균 검정처럼 1> 독립 표본인 경우와 2> 독립 표본이 아닌 경우로 나누어서 검정한다.
2) 독립 표본이 경우 이전 강의에 p 하나 가지고 했던 검정을 다시 떠올린다.
(https://intelligentcm.tistory.com/143)
=> 중심 극한 정리 써서 정규 분포로 검정한다.
3) PROC FREQ를 사용했다.
4) p1^-p2^를 Z로 표준화

기존 추정에서도 p1^, p2^, p1^-p2^ 모두 정규분포를 따른다.
그래서 p1^-p2^을 가지고 표준화를 해서 표준정규분포를 만든다.
하지만 그림에서 볼 수 있듯이 표준화 한 경우 분모에 p1과 p2가 너무 많아서 p1^, p2^로 각각 바꿨다.
10. 두 모집단 모비율 차에 대한 검정
1) 독립 표본에 의한 두 모비율 차의 비교
1> 조건
- 독립 => 문제 조건에서 판단한다.
2> Z로 표준화

- p1과 p2를 대체

추정의 경우 p1과 p2를 p1^, p2^로 각각 바꿨다. 그런데 검정에서는 약간 다른 점이 있다.
검정에서는 H0는 'p1-p2=0' 꼴로 두고 시작한다. 그리고 H0를 전제로 검정 통계량을 만든다.
=> 그래서 p1과 p2 모두를 p^으로 둡니다.
- p^에 대한 계산
모집단이 2개인데 하나의 p^을 계산하는 방법은

위와 같이 한 번에 계산하는 것이다.
3> 검정
- 우측 검정
p1-p2가 0보다 크다는 것을 증명하고 싶은 것이기 때문에 우측 검정이다.
z0가 zα보다 크다는 것을 증명하려고 한다.

- 좌측 검정

- 양측 검정

실제 PROC FREQ를 하면 양측 검정에 대한 결과가 나오므로 우측 검정과 좌측 검정을 하는 경우 약간의 계산이 필요하다.
cf> 복습
독립 표본인 경우 중심 극한 정리에 의해 정규 분포로 검정할 수 있다.
2) 짝표본에 의한 두 모비율 차의 비교 (McNemar 검정)
똑같은 사람에게 2개 이상의 조사를 한 결과를 분석

1> 귀무 가설
우리는 p_A와 p_B가 같은 지를 알고 싶다.


2> n_01의 분포
선호도 조사에서 문제 되는 것은 n_10와 n_01이다. (다른 제품에 대해서 다른 반응을 보이는 경우
n_01은 이항 분포를 따른다. 그래서 정규 분포에 근사할 수 있다. (by 중심 극한 정리)

3> 표준화

11. 두 모집단 모비율 차에 대한 검정 실습
1) 독립 표본에 의한 두 모비율 차의 비교
Bernoulli분포에서는 ~이다, ~ 아니다. => PROC FREQ
1> PROC FREQ
- tables 명령어 옵션 중 binomial (p=p0)를 사용 => 귀무 가설(H0) 설정
<이전 FREQ 복습>
(이 그림에서는 state가 범주가 되고, count를 뽑힌 횟수로 취급할 것입니다.)
- data=SAS-dataset : 사용할 data 선정
- order=data : 데이터에 제시된 순서대로 분석할 지 => 데이터에서 가장 먼저 나타나는 범주을 대상으로 분석
- weight variable_count : 정렬되어 있는 경우(현재 상황) 이 변수의 숫자를 뽑힌 횟수로 취급
- tables variable_category / binomial (p=p0) alpha=α :
- 이항비 table을 variable을 범주로해서 만든다. (variable_category에 대한 이항비 table)
- α는 추후 신뢰구간을 만들 경우 사용할 수 있다.
- tables의 다른 옵션
chisq : 피어슨의 카이제곱 통계량을 나타내라
(기대 빈도(np)가 5이하 인게 많으면 결과가 부정확할 수 있어서 아래 fisher를 사용한다.)
fisher :
(chisq와 fisher 모두 검정에 관한 옵션이니 단일 표본의 모비율 검정처럼 다른 옵션을 사용하지 안아도 된다.)
expected : 기대 빈도를 출력해준다.
2> 예시
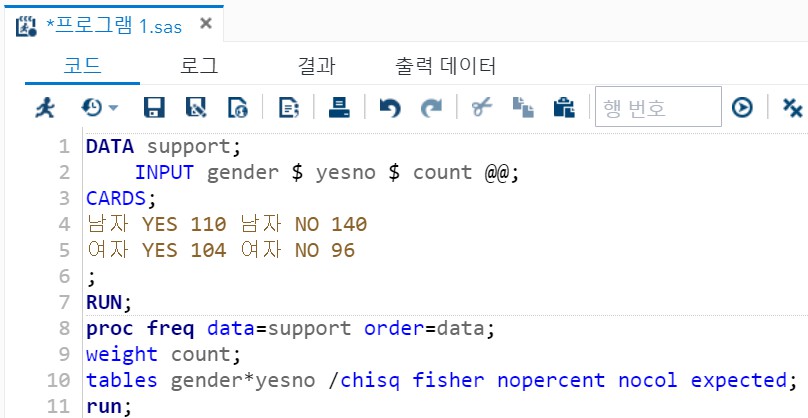
- 해당 표본은 독립 이표본이 맞다. => 표준 정규분포를 사용한다.
- order = data : YES가 맨 처음 등장하니 YES의 비중을 중심으로 검정
- weight = count : data가 이미 정렬된 상황이니 count 변수가 비율에서 분자에 해당하는 빈도임을 알려준다.
3> 결과 1

- expected 옵션을 사용해서 기댓 빈도도 출력한다.
ex> (p^ = (∑Xi + ∑Yi) / (m+n) )
남자 YES의 기댓값 : 110.89 = 250 * p^ | 여자 YES의 기댓값 : 95.111 = 200 * p^
남자 NO의 기댓값 : 131.11 = 250 * (1-p^) | 여자 NO의 기댓값 : 104.89 = 200 * (1 - p^)
(나중에 피어슨의 카이제곱 검정 통계량은 기대 빈도와 관측 빈도를 이용해서 계산한다.)
4> 결과 2

- 카이-제곱 검정 통계량
원래 검정 통계량 Z0는 표준 정규 분포에 근사해서
Z0를 제곱하면 χ2(1)의 분포를 가진다.
그래서 현재 카이제곱 검정 통계량은 2.8513을 가진다.
- 표준 정규 분포로 검정하는 경우
양측 검정을 하는 경우를 보면 H0 : p_1=p_2이기 때문에 빨간 부분에 검정 통계량이 들어가야 기각할 수 있다.

- 카이-제곱 분포로 검정하는 경우
하지만 카이-제곱 검정을 하면 모양이 조금 달라진다.

H0가 사실이면(p_1과 p_2가 같으면) Z_0가 점점 작아진다.
H1가 사실이면 Z_0가 점점 커진다.
그래서 Z_0^2을 가지고 카이-제곱 검정을 한다면 우측 검정이 된다.
- 결과 해석
prob이 0.0913 나왔는데 χ2_α(1)이 Z_0^2보다 클 확률이 0.0913이라는 뜻이다. (대소 관계 반대로 쓴 듯)
0.0913이니 10%의 유의확률로 기각할 수 있다.
4> 결과 3 - Fisher의 정확 검정
위의 결과 2로 검정을 햇을 때, 기대 빈도가 5 이하이면 정확하지 않을 수 있다.
(다행히도 위의 결과 1을 보면 모두 기대 빈도가 5를 넘는다.)

- 양측의 값이 0.1083이어서 결과 2에서 계산한 카이-제곱 분포 확률(0.0913)과 유사하게 나왔다.
2) 짝표본에 의한 두 모비율 차의 비교 (McNemar 검정)
2> 예제

- pre와 post : 전과 후에 대한 검정을 한다고 추측할 수 있다.
- exact mcnem : McNemar 검정을 할 때 쓴다.
3> 결과 1

- 카이-제곱 검정 통계량

- Pr > ChiSq (점근적인 Pr > S)
0.0007이기 때문에 1% 유의 수준으로도 기각할 수 있다.
=> 지지율 차이가 난다고 결론 내릴 수 있다.

혹시 표본의 크기가 적다고 생각할 수 있는데 expected 옵션을 넣어보면 기대 빈도가 모두 5%를 넘는 것을 확인할 수 있다.
'SAS' 카테고리의 다른 글
| 10-1강 - 일원 배치법 (0) | 2020.06.08 |
|---|---|
| 9-1강 - 범주형 자료의 분석 (0) | 2020.06.08 |
| [통계 개념&SAS] 8-4강 - 가설 검정 (독립이 아닌 모집단이 2개인 경우) (0) | 2020.05.12 |
| [통계 개념&SAS] 8-3강 - 가설 검정 (독립인 모집단이 2개인 경우) (0) | 2020.05.12 |
| [통계 개념&SAS] 8-2강 - 유의 확률 (p-value) (0) | 2020.05.07 |



