반응 변수와 설명 변수
2. ANOVA
일원 분류 분산 분석을 수행하기 위한 Procedure
균형 자료 (각 수준에서 반복수가 같은 경우) 사용
1) 문법
PROC ANOVA DATA='SAS-dataset'
ex> 온도 별 생산량을 조사
1> CLASS : 분류 변수 (설명 변수, 독립 변수) 지정 (x로 생각한다.) ex> 온도 지정
2> MODEL : 분류 변수와 반응 변수 지정 (y=x 꼴로 지정)
3> MEANS : 각 처리 수준별 표본평균 및 표준편차을 출력할 때 사용
- 다중 비교 옵션문 사용 가능하다.
- hovtest 에서 등분산성에 대한 검증을 할 수 있다. (homogeneous of variance) bartlett, levene 주로 사용
(기존에는 TTEST에서 했었다. 모집단이 2개인 경우)
- bartlett : 모집단이 정규 분포인 경우에만 사용할 수 있다.
- levene : 모집단이 정규 분포가 아닌 경우에도 사용할 수 있다.
2) 예제
1> 코드
DATA harvest;
INPUT fertile $ yield @@;
CARDS;
F1 148 F1 76 F1 134 F1 98
F2 166 F2 153 F2 255
F3 264 F3 214 F3 327 F3 304
F4 335 F4 436 F4 423 F4 380 F4 465
;
RUN;
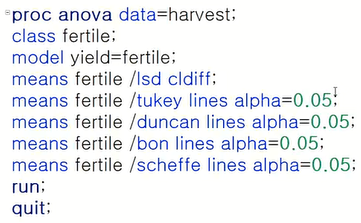
proc anova data=harvest;
class fertile;
model yield=fertile ;
means fertile/ lines alpha=0.01 lsd;
means fertile/ hovtest=bartlett;
run;
quit;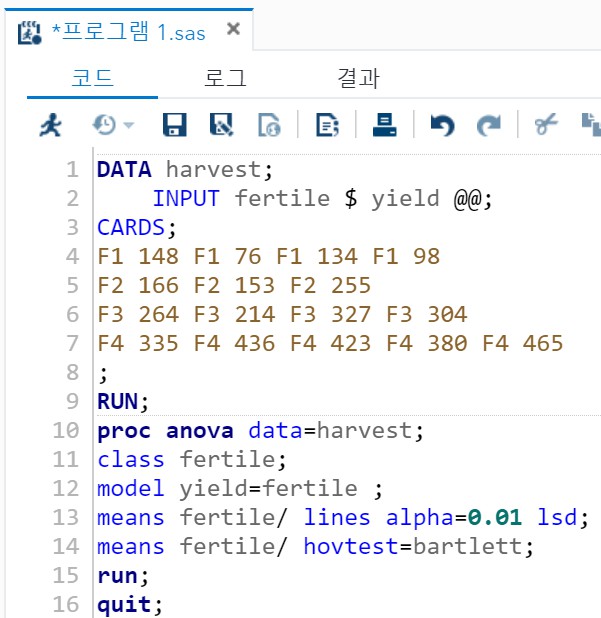
- model yield=fertile : yield를 반응 변수로 fertile을 독립변수로 지정
- means들 없이 실행하면 수준 효과가 있는지 없는지만 점검할 수 있다. (F 검정)
- quit : 간혹 사용해야 하는 경우가 있다.
2> 결과 1 (ANOVA 기본)

- class가 4종류 있다. (수준이 4개 있다.)
- 자료를 16개 읽어들여서 16개 사용했다.
3> 결과 2 (ANOVA 기본)
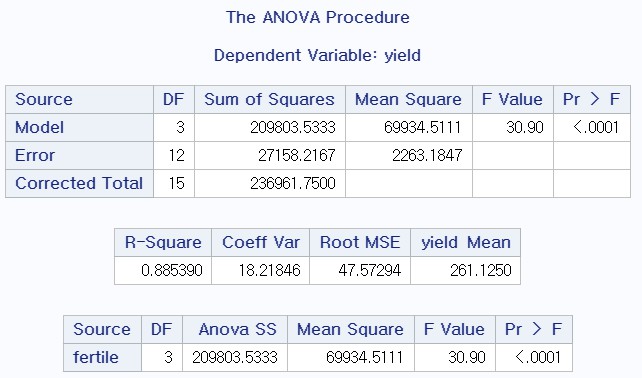
- 분산 분석표 (맨 위)
- 우측 검정시, 기각할 수 있다.
- yield Mean : 전체 평균
- 맨 아래는 나중에 이원 배치 분석에 사용
4> 결과 3 (ANOVA 기본)
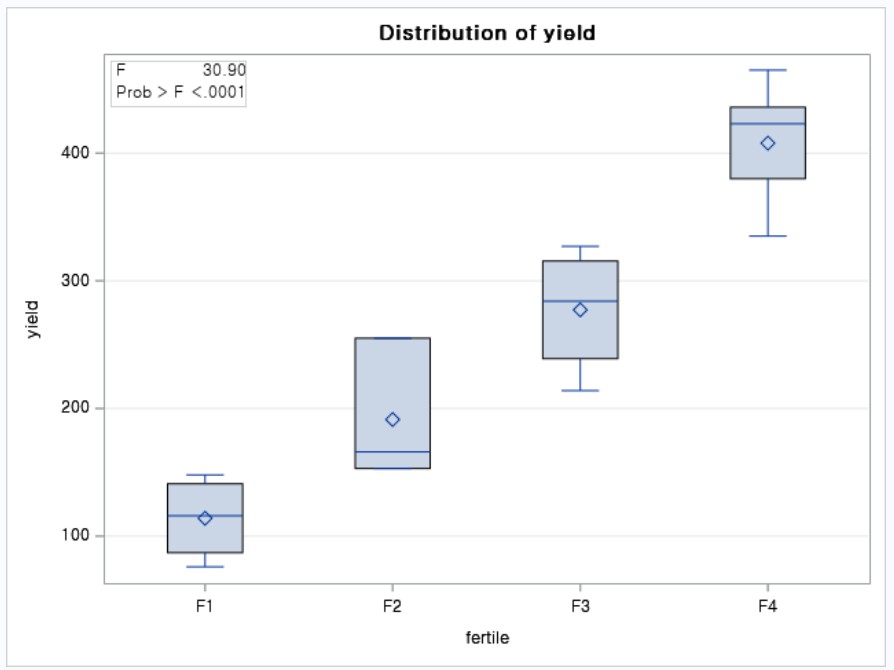
5> 결과 4 (means fertile / lines alpha=0.01 lsd)
lines : 표시 방법 (같은 범주 안에 들어가는 것은 같은 알파벳으로 표현)
(cldf : 2개의 차를 보여주는 표시 방법)
lsd도 검정이기 때문에 alpha를 지정해야 한다. (지정하지 않으면 0.05 수준에서 검정)
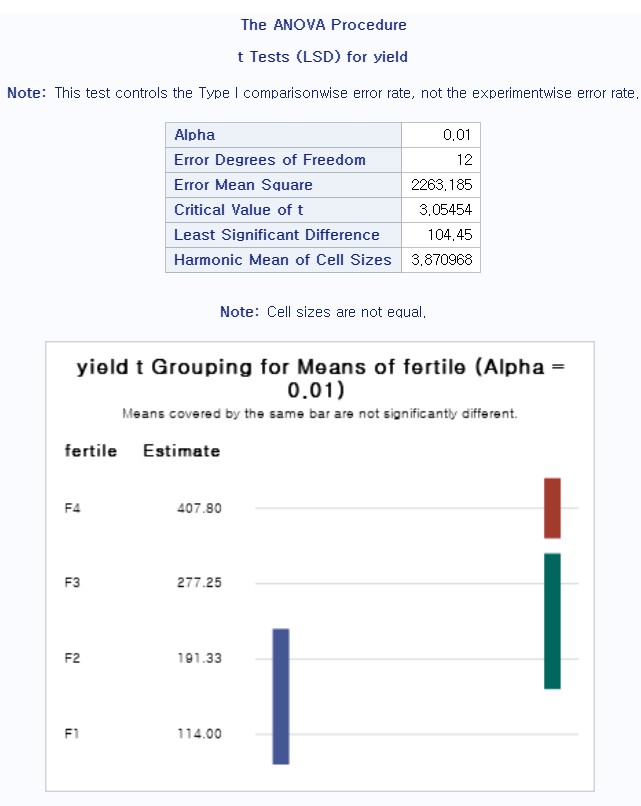

- 차이가 104.45를 넘어가면 유의한 차이가 있다고 할 수 있다.
- A는 F4 하나밖에 없다. => 어떤 것과도 같지 않다. (유의하지 않다.)
- B는 F3와 F2가 있다. => 1% 유의 수준에서 같다고 할 수 있다.
- C는 F2와 F1이 있다. => 1% 유의 수준에서 같다고 할 수 있다.
- 그렇다고 F1과 F3이 같은 그룹에 속하는 것은 아니다.
- 만약에 lines가 아니라 cldff를 옵션으로 사용하면 아래와 같이 표시한다.
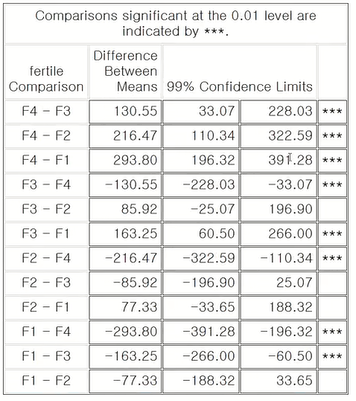
6> 결과 5 (means fertile/ hovtest=bartlett)
bartlett 방법으로 등분산에 관한 test도 시행
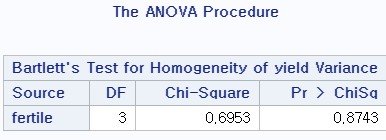
yield의 분산이 같은지에 대한 검정
- 카이-제곱 검정이며 우측 검정이다.
- 기각할 수 없다.
7> 결과 6 (means fertile/ hovtest=bartlett)
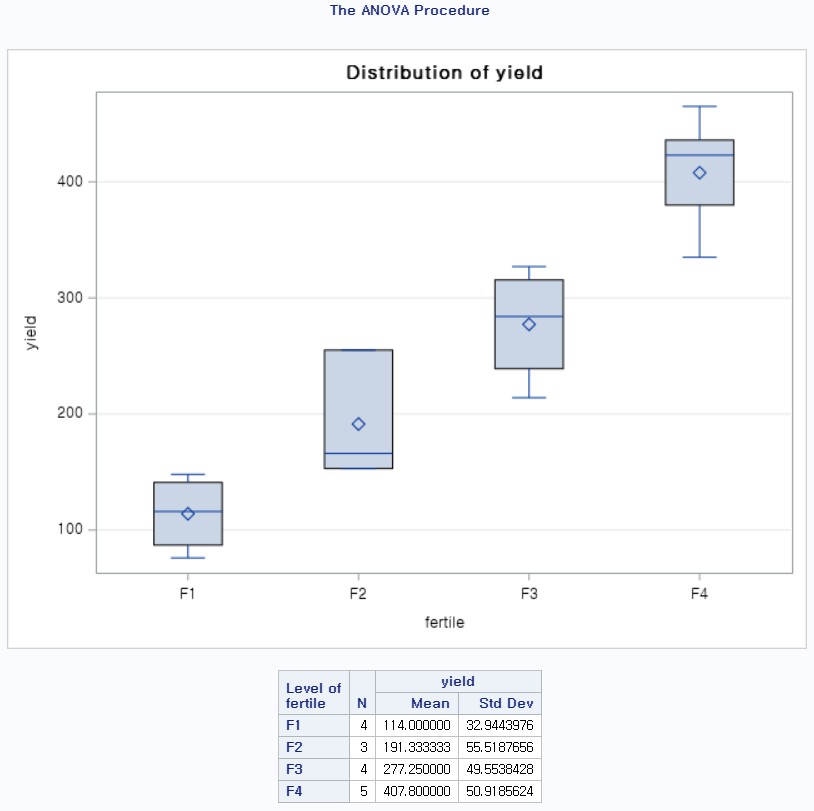
- F1~F4별로 평균과 표준편차를 출력
3) 추가적인 사후 검정
3. GLM
대비에 대한 것을 다룬다.
1) 예제
1> 코드
data ONEFAC;
do DENSITY=1 to 4;
input Y @@;
output;
end;
cards;
6250 6150 6080 6200
6300 6290 6120 6220
6420 6170 6020 6010
6220 6180 6040 6030
6320 6080 6020 6000
;
run;
proc glm;
class DENSITY;
model Y=DENSITY;
contrast '1 2 3 vs 4' density .3333 .3333 .3333 -1;
contrast '1 vs 2 3 4' density 1 -.33333 -.33333 -.33333
;
contrast '1 2 vs 3 4' density .5 .5 -.5 -.5;
contrast '1 vs 2 ' density 1 -1 0 0;
contrast '3 vs 4' density 0 0 1 -1;
means density/lsd;
run;
quit;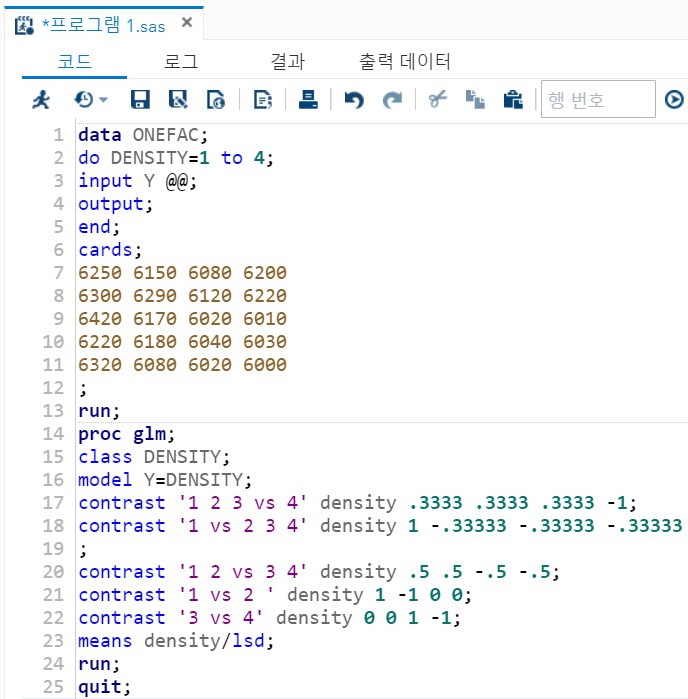
- do : 반복할 수 있다.
- do는 end로 끝나야 한다,
- input은 outpur으로 끝나야 한다.
- 처음 6250은 density가 1, 6150은 density가 2
- 이와 같은 원리로 density는 4개 있고 반복수는 5개 있다.
- contrast '명목형' density 비율 :
(최대한 소숫점을 많이 적어줘야 한다.)
2> 결과 1
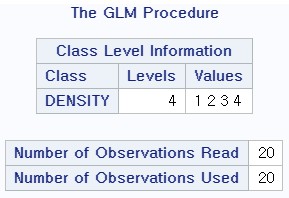
3> 결과 2
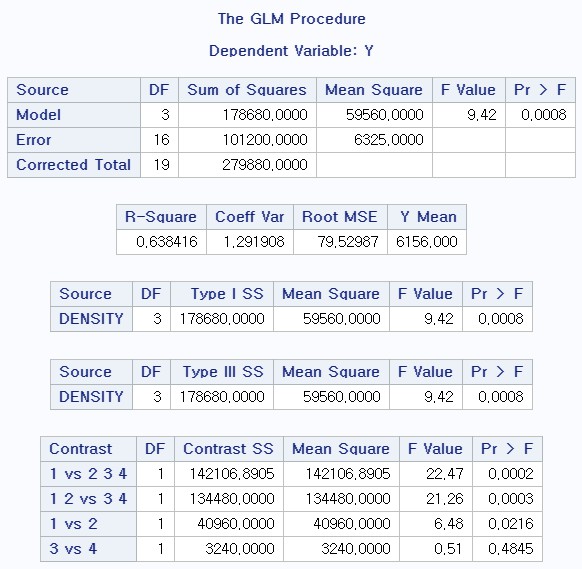
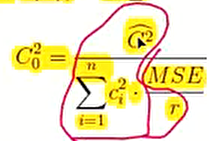
- t-value인 경우 양측 검정이고
- F-value인 경우 우측 검정이다.
- 빨간 부분이 Contrast SS이다.
'SAS' 카테고리의 다른 글
| [통계 개념] 11-1강 - 단순 선형 회귀 분석 (1) | 2020.06.08 |
|---|---|
| 10-3강 - 이원배치법 (0) | 2020.06.08 |
| 10-1강 - 일원 배치법 (0) | 2020.06.08 |
| 9-1강 - 범주형 자료의 분석 (0) | 2020.06.08 |
| [통계 개념&SAS] 8-5강 - 모비율 차에 대한 검정 (0) | 2020.06.08 |



