3. Asymptotic Notation
0) intro
1> step count를 세는 이유
- 동일한 함수가 다른 프로그램에서 시간 복잡도가 얼마나 다른지 비교하기 위해
- 인스턴스 특성이 변함에 따라 run time이 얼마나 변하는지 예측하기 위해
2> 정확한 step 시간 측정이 어려우며 step의 개념 자체가 부정확하기 때문에 앞서 이야기한 방식은 비교하는데 어려움이 있다.
1) Big "oh"
1> 정의
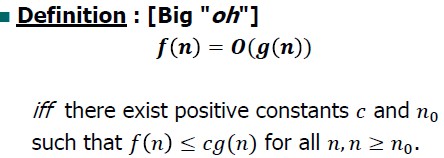
모든 n (n >= k) 에 대해
f(n) <= c g(n) 인 조건을 만족하는 두 양의 상수 c 와 k 가 존재하기만 하면
-> f(n) = 𝐎(g(n)) 이다.
2> 최악의 시간 복잡도
3> 상한을 의미한다.
4> 예제

2) Omega
1> 정의

모든 n (n >= k) 에 대해
f(n) >= c g(n) 인 조건을 만족하는 두 양의 상수 c 와 k 가 존재하기만 하면
-> f(n) = 𝛀(g(n))* 이다.
2> 최선의 시간복잡도
3> 하한
4> 예제

3) Theta
1> 정의
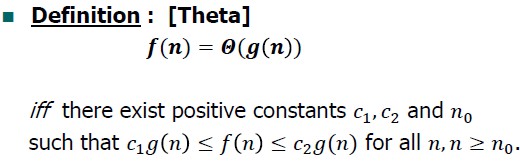
모든 n (n >= k) 에 대해
c₁ g(n) <= f(n) <= c₂ g(n) 인 조건을 만족하는 세 양의 상수 c₁, c₂ 와 k 가 존재하기만 하면
-> f(n) = 𝚯(g(n)) 이다.
2> 평균적인 시간 복잡도
3> 상한 & 하한
4> 예제

'자료구조' 카테고리의 다른 글
| 2-1강 - ADT array, 동적 할당 (0) | 2020.04.09 |
|---|---|
| 1-6강 - Performance measurement (시간 측정) (0) | 2020.03.31 |
| 1-5강 - Performance analysis (1) 공간 복잡도, 시간 복잡도 (0) | 2020.03.31 |
| 1-4강 - Data abstraction (0) | 2020.03.30 |
| 1-3강 - Algorithm specification (2) 재귀 알고리즘 (0) | 2020.03.30 |



