2. Euler Cycle(Path) Problem Solution 구현
1) Doubly Linked List Management
1> DBL Structure
아래 구조는 vertex에 대한 adjacent list이며
d에는 edge array의 index를 가지고 있다. (즉, 어떤 edge인지를 나타내는 것이다.)
typedef struct _DBL {
int d; // store edge array index
struct _DBL *twin; // the other DBL pointer
struct _DBL *lp , *rp; // reverse & forward ptr
} DBL;2> DBList class
class DBList {
private:
DBL *DBL_pool;
public:
unsigned long DBL_cnt;
unsigned long UsedMemoryForDBLs;
DBList (void) { // 생성자
DBL_pool = NULL;
DBL_cnt = 0;
UsedMemoryForDBLs = 0;
}
~DBList (void) {
}
DBL *allocDBL void;
void freeDBL (DBL *p);
void freeDBL_pool (void);
};cf>
생성자 : boycoding.tistory.com/244?category=1067100
소멸자 : boycoding.tistory.com/249?category=1067100
3> Member function - allocDBL
DBList와 달리 pool에는 singly linked list로 저장해도 된다.
- if (pool이 비어있는 경우) : system memory에서 메모리 가져온다.
- else (pool에 메모리를 가지고 있는 경우) : pool에서 메모리 하나를 추출한다.
- 그리고 가져오 메모리에 pointer를 모두 NULL로 초기화
- DBL에서 가져온 메모리 세기
DBL *DBList::allocDBL (void) {
DBL *p;
if (DBL_pool == NULL) { // pool=empty, call malloc
p = new DBL
if (p == NULL) {
Error_Exit("Memory alloc error(Alloc_DBL)");
}
UsedMemoryForDBLs += sizeof(DBL)
p->d = NONE;
}
else { // get an slm from the DBL_pool
p = DBL_pool;
DBL_pool = p -> rp ; // rp 를 사용하여 pool 연결
}
p->rp = p->lp = p->twin = NULL; // clear pointers
++DBL_cnt;
return (p);
}4> Member function - freeDBL
DBL에서 DBL_pool로 메모리를 보낸다.
void DBList freeDBL DBL *p) {
if (p->d == NONE) {
Error_Exit("This is already freed(Free_DBL)");
}
p->d = NONE;
p->rp = DBL_pool; // p rp points to DBL_pool
DBL_pool = p; // p becomes the 1st element
--DBL_cnt; // reduce # of active DBL
}5> Member function - freeDBL_pool
DBL_pool의 메모리를 system memory로 보낸다.
void DBList freeDBL_pool (void) {
DBL *p = DBL_pool;
while (p != NULL ) {
DBL_pool = p->rp;// get next pointer
delete p;
p = DBL_pool;
UsedMemoryForDBLs -= sizeof DBL;
}
if (DBL_cnt != 0) {
Error_Exit("Non zero DBL_cnt after cleanup");
}
}
2) DBL Stack
graph의 adjacent list 구성에 사용
1> DBL Stack class
class dblStack {
private:
DBL *ST;
public:
dblStack(void) {
ST = NULL;
}
~dblStack(void) {
}
void push(DBL *p);
DBL *pop(void);
void remove(DBL *p); // remove p from ST
DBL *top(void);
void empty(void); // true if empty
};2> Member function - remove
- stack 내에 어떤 위치에 있는 node를 제거 (pointer p를 argument로 사용해서) (내부 원소의 값을 확인해가다가 내가 제거하려는 값을 가진 node라면 제거한다.)
- twin link로 중복되는 다른 vertex의 adjacent edge로 이동해서 제거한다.
- 함수 종료후 제거한 node의 메모리는 freeDBL 함수를 통해 pool로 되돌려준다.
void dblStack::remove(DBL *p) { // rem p from ST
if (ST == p) { // p is the 1st element of ST
ST = p->rp; // assign p rp to Q (may be
if (p->rp != NULL) { // p is not the only elm
(p->rp)->lp = NULL; // p 우의 좌를 NULL
}
}
else { // p is not the 1st element
(p->lp)->rp = p->rp ; // p 의 좌의 우를 p 의 우로
if (p->rp != NULL) { // p is not last
(p->rp->lp = p->lp; // p 의 우의 좌를 p 의 좌로
}
}
}
3> Member function - push & pop
doubly linked list이기 때문에 기존에 SLL의 push & pop과 다른 점도 있다.
- push
- NULL이 아니면 먼저 ST가 가리키는 lp가 지금 들어온 p(node pointer)이게 하고 작업한다.
- pop
- 원소가 1개이면 pop 이후 ST를 아예 NULL로 만들고
- 원소가 1개 이상이면 [1] ST가 2번째 원소를 가리키게 하고 [2] 2번째 원소의 lp가 1번째 원소를 가리키지 못하게 한다.
void dblStack::push(DBL *p) {
if (ST != NULL) {
ST->lp = p; // link left pointer if Q != NULL
}
p->rp = ST;
p->lp = NULL;
ST = p; // p becomes the 1st element of Q
}
DBL *dblStack::pop(void) {
DBL *p;
p = ST;
if (ST->rp == NULL) {
ST = NULL;
}
else {
ST = ST->rp;
ST->lp = NULL;
}
return p;
}4> Member function - top & empty
DBL *dblStack::top(void) {
return ST;
}
bool dblStack::empty(void) {
if (ST == NULL)
return true;
else
return false;
}
3) Graph construction
1> adjacent list의 원소는 DBL이며
2> vertex 구조체의 dblStack에 원소를 저장한다.
typedef struct _Vertex {
dblStack S;// adj list contains edge index
int degree;
} Vertex;
typedef struct _Edge {
int v1, v2;
} Edge;
cf> Euler Cycle/Path Finding 정리
1> 탐색을 통해 모든 vertex의 degree를 조사 -> 시작 vertex s를 결정
2> cycle C를 찾고,
3> C 내부의 vertex를 조사하여, 방문하지 않은 edge를 incident edge로 가지는 vertex에서 cycle C'를 찾는다.
4> 이를 끼워넣는다.
5> 3>~4>를 반복한다.
(위 방법은 edge를 2번씩 방문해야 하므로 좀 더 효율적인 방법을 고민해본다.)
4) 효율적인 방법 pseudo-code
1> p : Euler cycle(path) 저장 용도
- path이면 |V|
- cycle이면 |V| + 1
2> 먼저 start vertex를 S에 넣어주고 S가 empty일 때까지 반복한다.
3> degree(v) == 0이면 (더 이상 갈 곳이 없으면),
- v를 P에 추가하고 S에서 제거한다.
4> degree(v) != 0이면 (갈 곳이 남아있으면),
- v와 incident edge를 하여 e를 graph에서 제거한다.
- 그리고 w로 이동했으니 w를 S에 push한다.

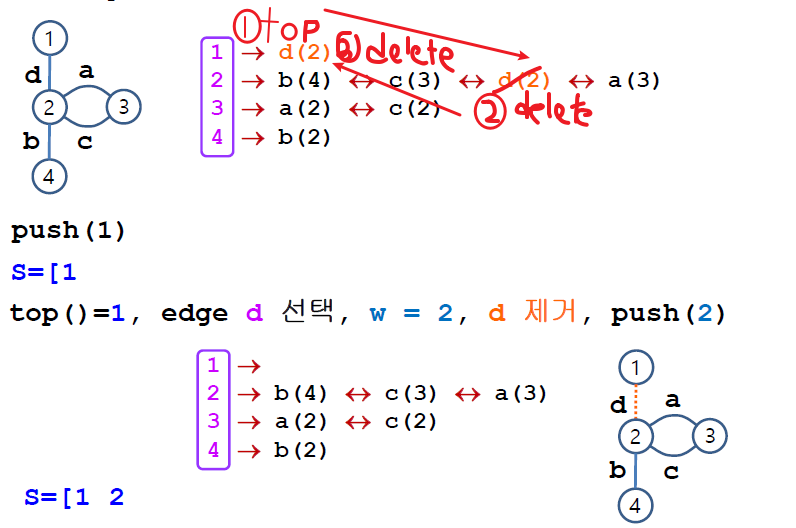
5) pseudo-code 예시

1> first vertex 설정 및 S.push(1)
2> else(갈 곳 2가 있다.)이니
[1] edge d 제거 (3 step : 1의 top으로 접근 → link로 반대편 원소 제거 → 다시 link로 돌아와서 남은 원소 제거)
[2] S.push(2)
6) 결론
결론적으로 해당 pseudo-code는
[1] cycle(path) 탐색을 하다가
[2]
- edge가 있으면 해당 vertex를 stack에 push
- 더 이상 갈 곳이 없으면 pop해서 path에 넣는다. (backtracking)
[3] 그리고 다시 갈 곳이 보이면 stack에 push
[1]~[3]이 DFS와 유사하다.
'알고리즘 > 알고리즘_학교' 카테고리의 다른 글
| 6-1강 - Dynamic Programming 1 (DP, Binomial Coefficient) (0) | 2020.11.11 |
|---|---|
| 5-1강 - Divide and Conquer 0 (Solving Recurrences Equations) (0) | 2020.10.23 |
| 4-1강 - Euler's path(cycle) 1 (개념 정리 및 구현 아이디어) (0) | 2020.10.09 |
| 3-2강 - 자료구조 & C, C++ programming 2 (Linked List management, Stack & Queue) (0) | 2020.10.03 |
| 3-1강 - 자료구조 & C, C++ programming 1 (call by reference, dynamic allocation) (0) | 2020.10.03 |



