0. Review
walk : vertex와 edge가 교대로 나타나는 sequence (sequence 내의 edge는 앞 뒤의 vertex를 이어야 한다.)
| walk | edge 중복 불가 | vertex 중복 불가 | v_0 = v_n | |
| walk | O | X | X | X |
| trail | O | O | X | X |
| path | O | O | O | X |
| cycle | O | O | O | O |
| closed walk | O | X | X | O |
| closed trail | O | O | X | O |
1. Euler Cycle(Path) Problem
1) 문제 소개
1> 크게 아래 3가지 경우로 나눌 수 있다.
- [1] Euler cycle이 존재하거나
- [2] Euler path만 존재하거나
- [3] 아무것도 존재하지 않거나

2> 이들을 판단하는 조건
vertex degree (d(v)) : 각 vertex v에 incident하는 edge의 개수
2) Euler cycle(path)가 존재하기 위한 필요조건
(사실 충분조건이기도 해서 필요충분조건입니다. 하지만 충분조건 증명은 다소 길고 복잡해서 생략합니다.)
1> Euler cycle의 필요(충분)조건
Graph의 [1] 모든 vertex degree가 짝수라면, Euler cycle이 존재한다.
2> Euler path의 필요(충분)조건
Graph에서 [1] 2개의 vertex degree가 홀수이고 [2] 나머지 vertex가 짝수라면, Euler path가 존재한다.
※그러므로 우리는 이제 vertex를 search할 필요가 있습니다.
3) Euler cycle(path) 찾기
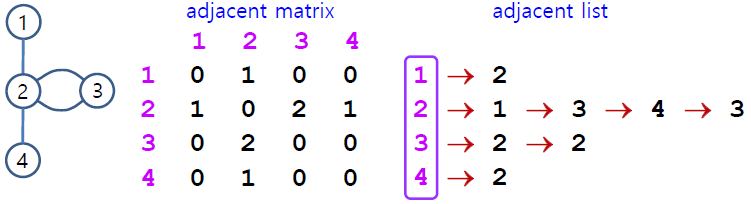
1> Vertex degree check 접근법 2가지 (adjacent matrix vs adjacent list)
G의 vertex 개수 : n, G의 edge 개수 : m
| adjacent matrix | adjacent list | |
| checking degree complexity | O(n^2) | O(m) |
2> Euler cycle
- 임의의 vertex v에서 시작
- 임의로 edge 선택해서 다음 vertex 이동 -> 반복
- 처음 vertex v로 돌아온다.
3> Euler path
- 홀수 degree vertex에서 시작
- 임의로 edge 선택해서 다음 vertex 이동 -> 반복
- 또 다른 홀수 degree vertex로 돌아온다.
4> 문제점 1 : 하지만 모든 vertex, edge를 지나는 cycle 혹은 path를 찾지 못할 수도 있습니다.
4) 문제점 1에 대한 해결
0> 간단한 개요
- [1] 찾은 cycle(path) C_0 내에 미사용 incident edge가 있는 vertex가 있을 수 있다.
- [2] 기존 cycle(path) C_0을 제외하고 미사용 edge들을 고려한 cycle(path) C_1를 찾는다.
- [3] 그리고 C_1을 C_0에 삽입한다.
1> 일반화 ([1], [2])
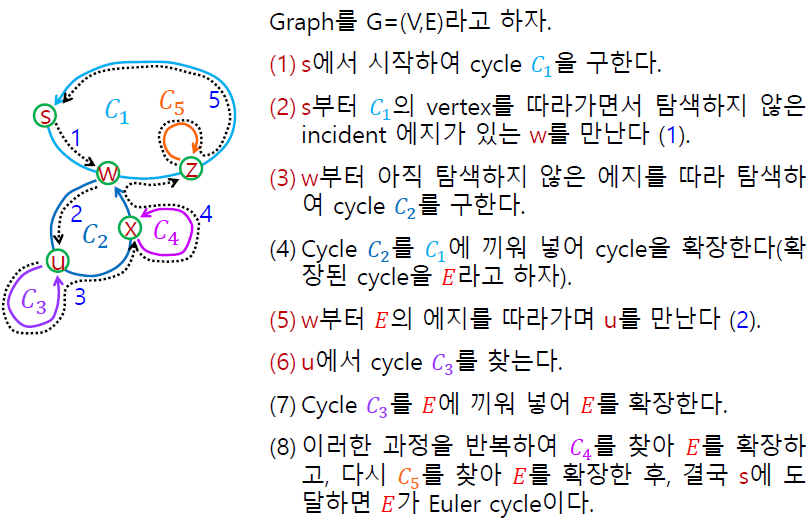
2> 삽입 ([3])
linked list 삽입으로 구현한다.
3> 예시
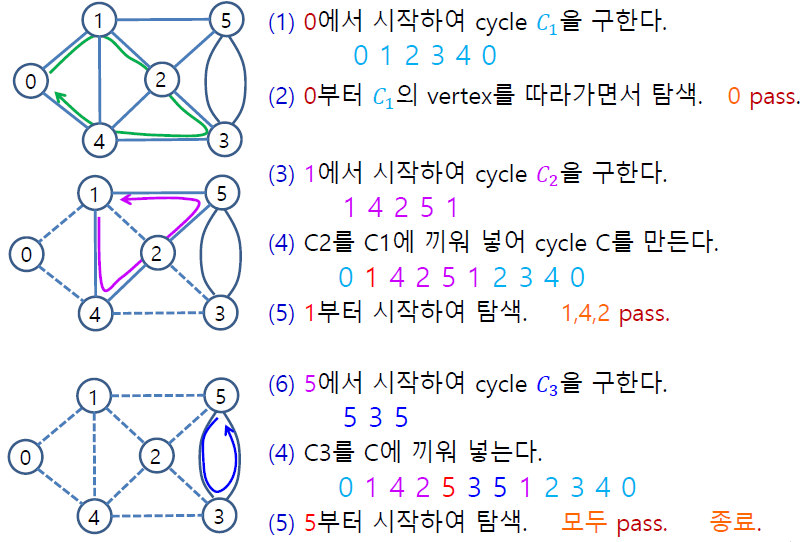
5) 문제점 1 해결에 대한 Data Structure 구현 idea
1> adjacent matrix 접근 (비효율적)
모든 vertex(row)를 search해야하기 때문에 complexity가 O(n)이다.
2> adjacent list 접근 - 지나온 edge 보존 & flag 사용 (비효율적)
지나온 edge를 보존하면 complexity가 O(degree(v))이다.
3> adjacent list 접근 - 지나온 edge 삭제 & singly linked list 사용 (비효율적)
내부 삭제는 따라가면서 지워야 하므로 시간이 필요합니다.
4> adjacent list 접근 - 지나온 edge 삭제 & doubly linked list 사용
list 원소를 O(1)에 삭제할 수 있다.
(왜 doubly를 사용하면 시간적으로 단축이 되지???)
6) 문제점 2 : undirected graph의 edge는 adjacent list에서 원소를 2번 지워야 한다.
1> 해결 : 중복된 두 원소 간에 서로 링크를 만든다.

7) 최종 Graph Data Structure

'알고리즘 > 알고리즘_학교' 카테고리의 다른 글
| 5-1강 - Divide and Conquer 0 (Solving Recurrences Equations) (0) | 2020.10.23 |
|---|---|
| 4-2강 - Euler Cycle(Path) 2 (구현) (0) | 2020.10.09 |
| 3-2강 - 자료구조 & C, C++ programming 2 (Linked List management, Stack & Queue) (0) | 2020.10.03 |
| 3-1강 - 자료구조 & C, C++ programming 1 (call by reference, dynamic allocation) (0) | 2020.10.03 |
| 2-1강 - Algorithm & Complexity 1 (알고리즘의 정의) (0) | 2020.09.15 |



