cf> 카르노맵 주의사항
1) b'd' 부분 확인하기 (자주 놓쳐서)
2) 그 외 모서리 부분을 공유하는 부분 항상 주의하기
1. Review
1) 정의들
1> Boolean function

2> letter : constant (0, 1) or variable (x,...)
3> literal : letter, its complement

2) Product term & Sum term
1> Product term
- 기본적으로 값이 1이다. (0이면 다른 어떤 값을 곱해도 0이 되어버리기 때문이다.)
- non-constant literal이 존재
- 같은 non-constant literal에 대한 conjunction(곱셈)이 2번이상 나오면 안 된다.

(4번째 예시는 x1과 x1'이 모두 곱셈에 들어가 있으므로 non-constant literal이 2번 이상 등장해서 product term이 아니다.)
(5번째 예시는 conjunction이 아니라 disjunction(합항)이기 때문에 product term이 아니다.)
2> Sum term
- 기본적으로 값이 0이다. (1이면 다른 어떤 값을 더해도 1이 되어버리기 때문이다.)
- non-constant literal이 존재
- 같은 non-constant literal이 2번이상 나오면 안 된다.

(4번째 예시는 disconjunction이 아니라 conjunction(곱항)이기 때문에 sum term이 아니다.)
(5번째 예시는 x1과 x1'이 모두 덧셈에 들어가 있으므로 non-constant literal이 2번 이상 등장해서 sum term이 아니다.)
3) Minterm & Maxterm
1> Minterm
: [1] 모든 변수가 항상 한 번씩 사용된 [2] product term

2> Maxterm
: [1] 모든 변수가 항상 한 번씩 사용된 [2] product term
3> Minterm & Maxterm 예시

4) Boolean function을 나타태는 방식
1> SOP, DNF, ∑∏ (sum of product, disjunctive normal form)

(위 예시는 canonical form은 아니다.)
2> POS, CNF, ∏∑ (product of sum, conjunctive normal form)

3> canonical SOP : sum of minterm
SOP 형태에서 모든 변수가 사용되어야 한다.

4> canonical POS : sum of minterm
POS 형태에서 모든 변수가 사용되어야 한다.

2. The Karnaugh Map
1) 용어

1> Implicant (항) : 함수 내에 포함될 수 있는 product term들 (카르노 맵에서 1이나 1들로 만들 수 있는 사각형집합)
2> Prime Implicant (필수 항) : 더 큰(다른) 묶음에 포함되지 않는 묶음 (더 이상 하나로 합쳐질 수 없는 Implicant)
- 위 그림에서 보면 ab'c'와 abc'는 ac'로 합쳐질 수 있기 때문에 Prime Implicant가 아니다.
- 그러나 a'b'c와 a'cd'는 하나로 합쳐질 수 없기 때문에 Prime Implicant이다.
3> Essential Prime Implicant
[1] 하나의 prime Implicant를 형성하고 있는 1 들 중에서
[2] 모든 PI가 다른 Implicant에 속하지 않고 자신의 Prime Implicant 묶음에만 속하는 관계
(간단히 다른 Implicant에 속하지 않는 부분을 떠올려도 된다.)
- 일단 왼쪽 하단에서 a'b'c와 a'cd'에 모두 속하는 1은 ESI가 아니지만
- 그 외의 1 2개는 다른 PI에 속하지 않기 때문에 ESI이다.
4> 간략화된 함수에는 Essential Prime Implicant와 non-Essential Prime Implicant 일부를 포함
(꼭 EPI만의 합이 아니어도 간략화 할 수 있는 예시)
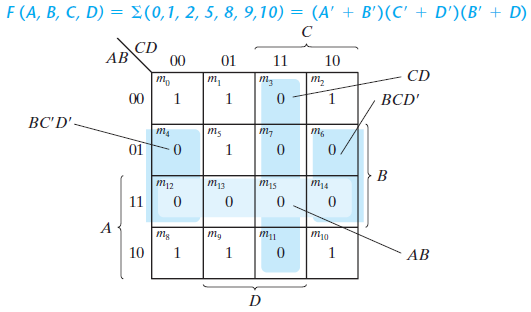
2) 예제

BC와 AC'는 둘 다 PI이며 서로 교집합이 없으므로 EPI(Essential Prime Implicant)이다.
3) Optimization Algorithm
1> prime implicant 모두 찾기
2> essential prime implicant도 모두 찾는다.
3> Select a minimum cost set of non essential prime implicants to cover all minterms not yet covered:
– Obtaining an optimum solution: See Reading Supplement More on Optimization
– Obtaining a good simplified solution: Use the Selection Rule
4) 카르노 맵과 SOP & POS와의 관계

1> K-map -> SOP
K-map의 1들을 묶어주면 SOP(AND-OR 꼴)가 된다.
2> K-map -> POS
K-map의 0들을 묶어주면 F'의 SOP 꼴이고
이를 complement처리를 하면 F의 POS(AND-OR)를 구할 수 있다.

5) 카르노 맵 예시
1> 2 variable map


2> three-variable map

3. Karnaugh Map 실전
1) 1을 묶는 법
1> 3-, 4- variable map의 묶는 방향 : 기본적으로 상하좌우가 가능하지만 3-variable에서는 그렇지 않은 경우 존재

2> 묶는 원칙 : 가능하면 크게 묶는다. (그리고 점차 세밀한 부분을 묶는다.)
3> 묶고 난 결과 : 어떤 값에 관계가 없는지 확인한다.

- 빨간 부분은 x, y의 값에 관계없이 z가 1이다. → z
- 파란 부분은 y, z의 값에 관계없이 x가 1이다. → x

- 빨간 부분은 z값에 관계없이 x와 y가 모두 0(complement)이다. → x'y'
- 파란 부분은 x값에 관계없이 y와 z가 모두 1(original)이다. → yz
- 초록 부분은 y값에 관계없이 x는 1이고, z는 모두 0이다. → xz'
4> 효율성에 대한 생각

이와 같이 묶으면 1이 혼자서 묶이는(xyz)경우가 생긴다.
3-input AND gate가 필요하다.
하지만 3-input AND gate는 매우 큰 unit이어서 좋지 않다.
그래서 최대한 크게 묶는 게 좋다.

(다른 표현이지만 같은 truth table을 가진다.)
5> 4 variable example

6> 여러 조합을 생각해보는 방법

최대한 EPI 먼저 고려한다.
7> 5-variable map
4-variable map이 2개있다고 생각하면 된다.
(내 생각 : 3D-array 형태를 생각해도 될 것 같다.)

2) Don't care
사용되지 않는 minterm을 don't care로 표시하고
이를 0이나 1로 내 맘대로 사용한다.

3) carry와 함께 연산





