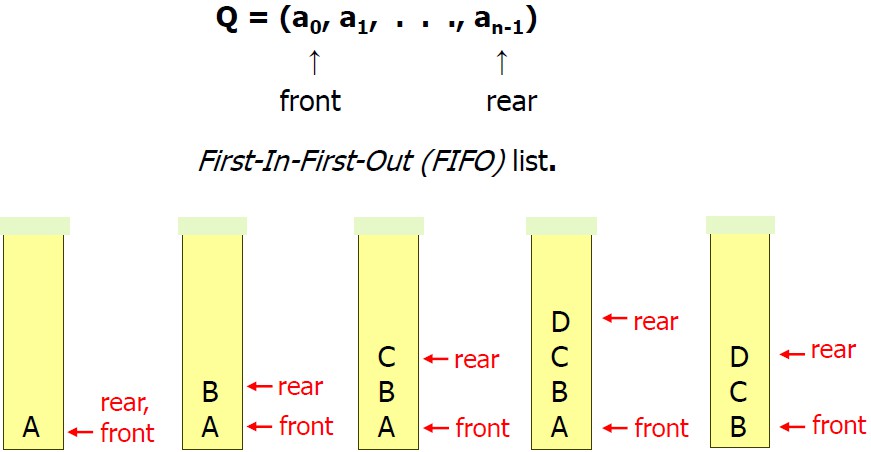
3. Queue
1) 개념
1> rear에서만 삽입이 일어나 front에서만 삭제가 일어나는 ordered list
2> FIFO(First in First out) : 제일 먼저 들어온 것이 제일 먼저 삭제
3> 삽입 : add = put = push = insertion
4> 삭제 : delete = pop = removal
2) ADT Queue
1> object : 0개 이상의 element를 가지는 finite ordered list
2> function
- Queue CreateQ(maxQueueSize) : 최대 크기가 maxStackSize인 empty queue 생성
- Boolean IsFullQ(queue, maxQueueSize) : 원소의 개수가 maxQueueSize이면 true, 아니면 false
- Queue AddQ(queue, item) : IsFullQ로 비었는지(true) 확인하고, 비어있다면(false) item을 queue의 rear에 삽입
- Boolean IsEmptyQ(queue) : queue가 CreateQ로 만든 empty queue과 같으면 true, 아니면 false
- Element DeleteQ(queue) : IsEmptyQ로 확인, 비어있다면 return으로 종결, 아니면 front에 있는 item을 삭제하고 return

3) 구현
0> 구현에서 먼저 고려할 것
- 1-dimensional array와 2개의 variable(front, rear)를 가져야 한다.
- front는 첫 번째 원소, rear는 마지막 원소를 지칭한다.
- 그리고 'front == rear'는 queue가 비었는지 확인할 때 사용할 수 있다.
1> Queue CreateQ(maxQueueSize)
- 정수 값을 가지는 (경우에 따라 다른 field를 가질 수 있다.) element 구조체를 만든다.
- MAX_QUEUE_SIZE개의 element를 원소로 가지는 array를 생성 (queue)
- front와 rear의 index를 저장할 변수를 선언하고 이를 -1로 초기화한다.
#include <stdio.h>
// Queue CreateQ(maxQueueSize)
#define MAX_QUEUE_SIZE 100 /* maximum queue size */
typedef struct
{
int key;
/* other fields */
}element;
element queue[MAX_QUEUE_SIZE];
int front = -1;
int rear = -1;
// Boolean IsEmptyQ(queue) :: = front == rear;
// Boolean IsFullQ(queue) :: = rear == MAX_QUEUE_SIZE-1;
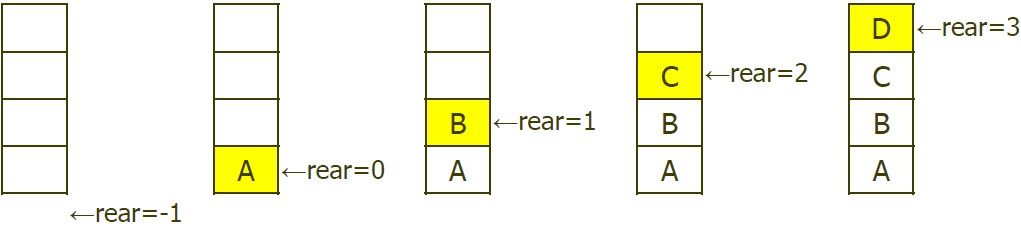
2> void addq(element item)
(full 검사 -> (nonfull) rear 증가 -> item 삽입)
- 해당 queue가 꽉 차 있는지 확인 ('rear == MAX_QUEUE_SIZE-1'로 확인 -> 같다면 queueFull()로 에러메시지 출력)
- 그렇지 않다면 (증가 -> 삽입)
- rear를 1 증가시키고 (증감 연산자를 앞에 붙인다.)
- 해당 index(rear)에 item을 추가한다.
void addq(element item)
{/* add an item to the queue */
if (rear == MAX_QUEUE_SIZE-1)
queueFull();
queue[++rear] = item;
}
3> element deleteq()
(empty 검사 -> (nonempty) front 증가 -> element return)
- 해당 queue가 전부 비어 있는지 확인 ('front == rear' 확인 -> 같다면 return queueEmpty() )
- 그렇지 않다면 (증가(삭제) -> 출력)
- front를 1 증가시킨다. (queue의 맨 앞 원소가 하나 사라진다.)
- queue에서 front가 1 증가된 index에 있는 원소를 return (현재 front가 가리키는 원소는 바로 직전에 제거되었고 현재 queue에 포함되는 원소가 아니다. 즉, 이전 원소를 return 하는 것이다.)

cf> job scheduling 예제

- 큐는 컴퓨터 프로그래밍에서 많이 사용한다. 큐의 가장 보편적인 이용은 운영 체제에 의한 작업 큐(job queue)의 생성이다. 만약 운영 체제가 우선순위를 사용하지 않는다면 작업들은 시스템에 들어간 순서대로 처리될 것이다.
- queue에 값이 들어가고 나감에 따라 -> queue는 점차 오른쪽(rear)으로 이동한다.
- queueFull을 만족하려면 전체 queue는 왼쪽으로 이동시켜야 한다. (안 그러면 오른쪽만 꽉 찬 형태가 된다/)
- 하지만 이 이동(전체 queue를 왼쪽으로 이동)은 시간이 많이 걸린다. (최악의 경우 시간 복잡도 O(MAX_QUEUE_SIZE))
- queue가 array의 끝을 둘러싸도록 해보면 queue를 더 효율적으로 표현 가능
4) 효율적 구현 : circular queue
0> 개념
- front : first element에서 반시계 방향으로 한 칸 이동한 index (위에서 front 정한 것처럼 바로 직전 index 가리킨다.)
- rear : element가 존재하는 index 중 마지막 index
- 이제 queueFull을 만족시키기 위해 배열의 element를 이동시키지 않아도 된다.
- 부연
- 배열이 하나의 원으로 구성되면 모든 배열의 element는 앞과 뒤의 위치를 가지게 된다.
- MAX_QUEUE_SIZE-1의 다음 위치는 0 / 0의 뒤는 MAX_QUEUE_SIZE -1
- queue의 rear가 MAX_QUEUE_SIZE -1에 있게 되면 다음 element는 위치 0에 삽입된다.
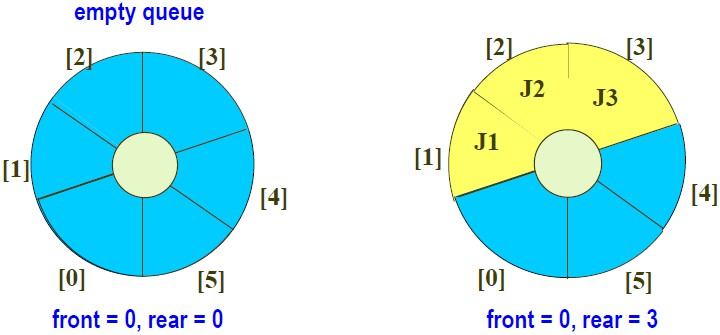
- 구현 시에 주의 : circular rotation (front, rear의 index가 커지다가 MAX_QUEUE_SIZE-1을 초과하면 modulus로 변경)
- empty queue == (front == rear) [delete 전에 확인]
- full queue == (front == rear) [add 전에 확인]
- empty와 full 검사가 겹치는 걸 방지하기 위해
- (add 하기 위해) full 검사 전에 rear를 먼저 증가시키고
- (delete 하기 위해) empty 검사 후에 front를 증가시킨다 (기존의 방식)
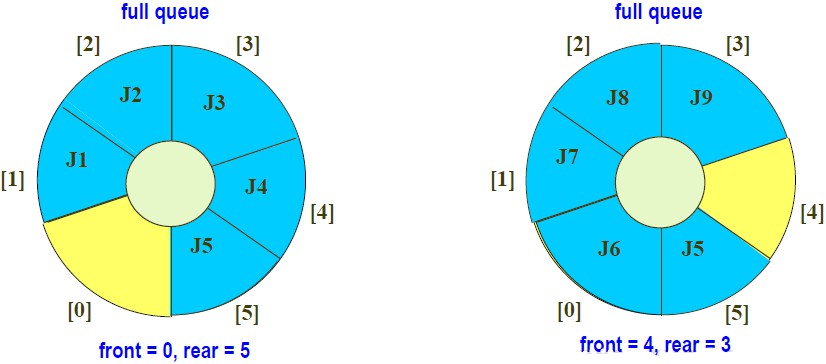
- 이와 같이 2가지 경우로 full queue가 된다.
1> circular queue 생성
- 정수 값을 가지는 (경우에 따라 다른 field를 가질 수 있다.) element 구조체를 만든다.
- MAX_QUEUE_SIZE개의 element를 원소로 가지는 array를 생성 (queue)
- circular queue는 1번째 index부터 채워넣을 것이다.
- front와 rear의 index를 저장할 변수를 선언하고 이를 0으로 초기화한다.
#include <stdio.h>
// Queue CreateQ(maxQueueSize)
#define MAX_QUEUE_SIZE 100 /* maximum queue size */
typedef struct
{
int key;
/* other fields */
}element;
element queue[MAX_QUEUE_SIZE];
int front = 0;
int rear = 0;
// Boolean IsEmptyQ(queue) :: = front == rear;
// Boolean IsFullQ(queue) :: = rear == MAX_QUEUE_SIZE-1;
2> add to a circular queue
(rear 증가 -> modulus -> full 검사 -> 삽입 or 에러메시지)
- 먼저 rear를 1 증가시키고 MAX_QUEUE_SIZE-1보다 rear가 커졌을 때를 대비해 modulus 연산을 가한다.
- 해당 queue가 꽉 차 있는지 확인 ('front == rear'로 확인 -> 같다면 queueFull()로 에러메시지 출력)
- 그렇지 않다면 증가된 index(rear)에 item 삽입
void addq (element item)
{ /* add an item to the queue */
rear = (rear + 1) % MAX_QUEUE_SIZE;
if (front == rear)
queueFull(); /* print error and exit */
queue[rear] = item;
}
3> delete from a circular queue
(empty 검사 -> front 증가 -> modulus -> return or 에러 메시지)
- 해당 queue가 비어있는지 확인 ('front == rear'로 확인 -> 같다면 queueEmpty()로 에러메시지 출력)
- 그렇지 않다면 -> front 1 증가 -> modulus 연산 -> return queue[front] (제거된 원소 return)
(front는 현재 맨 앞 원소 이전의 index이니까)
element deleteq()
{ /* remove element at the front of the queue */
if (front == rear)
return queueEmpty() /* return an error key */
front = (front + 1) % MAX_QUEUE_SIZE;
return queue[front] // 방금 제거된 원소를 return
}
4. Circular Queue using Dynamic Allocated Arrays
1) 개념
1> circular queue가 꽉 찰 때마다 realloc으로 메모리를 2배로 재할당한다.
(하지만 실제로는 malloc으로 구현하는 게 효율적이어서 구현은 malloc으로 진행한다.)
- capacity : 현재 element의 개수 (초기에 1로 설정한다.)
2> 하지만 원형 구조 특성상 메모리가 2배될 때 재배열이 필요하다.
- 메모리, capacity 2배로 만든 뒤 (newQueue 생성)
- front 이후의 원소(front+1 ~ capacity-1)들은 newQueue의 0번째 index부터 복사하여 넣는다. (capacity-front-1개)
- front 이전의 원소(0 ~ rear)들은 newQueue의 capacity-front-1 부터 복사하여 넣는다.

2) 구현
1> queueFull() : 꽉 찼을 때 메모리를 증가시키고 재배열
- newQueue에 기존 queue의 2배의 메모리를 동적 할당(malloc)
- start(첫 번째 원소의 index)는 front에 1을 더하고 modulus 연산을 가하면 얻을 수 있다.
- segment 분할 여부 조사 ( start < 2 이면 segment가 1개이다.)
- (segment 분할이 안 된 경우) 그대로 start~start+capacity-1까지 newQueue에 복사한다.
- (segment 분할이 된 경우)
- 2번째 segment(start~capacity)를 newQueue의 맨 앞(0)부터 채워넣는다.
- 1번째 segment(0~rear+1<rear+1은 빈칸>)를 newQueue의 capacity-start index부터 채워넣는다.

- queue에서 newQueue로 이동하면서 바뀐 것들
- front를 newQueue의 마지막 index로 변경 (기존 linear queue 초기화 방식을 갑자기 따른다.)
- rear는 newQueue의 절반에서 빈칸을 1개 확보한 자리로 index 변경 (절반 부분은 capacity-1이고 빈칸 확보하자)
- 이제 capacity도 2배로 증가시킨다.
- queue의 메모리 해제
- newQueue의 이름을 queue로 변경
#include <stdio.h>
#include <stdlib.h>
#define MAX_QUEUE_SIZE 100 /* maximum queue size */
typedef struct
{
int key;
/* other fields */
}element;
element queue[MAX_QUEUE_SIZE];
int front = 5;
int rear = 5;
int capacity = 8;
void queueFull()
{
/* 2배의 메모리 할당 */
element* newQueue;
newQueue = (element *)malloc(2 * capacity * sizeof(*queue));
/* copy from queue to newQueue */
int start = (front + 1) % capacity; // front : 첫 번째 원소가 있는 index
if (start < 2) /* 위의 그림처럼 2개의 segment가 생기지 않은 경우 */
copy(queue + start, queue + start + capacity - 1, newQueue);
// 그냥 차례대로 newQueue에 복사하면 된다.
else /* 위의 그림처럼 2개의 segment가 생긴 경우 */
{
copy(queue + start, queue + capacity, newQueue);
// 2번째 segment(front 이후 원소들)는 newQueue 맨 앞 부터 채워 넣는다.
copy(queue, queue + rear + 1, newQueue + capacity - start);
// 1번째 segment(front 이전 원소들)는 2번째 segment가 채워진 이후부터 채워진다.
}
/* newQueue로 복사되면서 바뀐 정보들 변경*/
front = 2 * capacity - 1;
rear = capacity - 2;
capacity *= 2;
free(queue);
queue = newQueue;
}2> void addq(element item)
(rear 증가 -> modulus -> full 검사 -> 삽입 or 에러메시지)
- 먼저 rear를 1 증가시키고 MAX_QUEUE_SIZE-1보다 rear가 커졌을 때를 대비해 modulus 연산을 가한다.
- 해당 queue가 꽉 차 있는지 확인 ('front == rear'로 확인 -> 같다면 queueFull()로 에러메시지 출력)
- 그렇지 않다면 증가된 index(rear)에 item 삽입
void addq(element item)
{ /* add an item to the queue */
rear = (rear + 1) % capacity;
if (front == rear)
queueFull(); /* double capacity */
queue[rear] = item;
}'자료구조' 카테고리의 다른 글
| 3-4강 - Evaluation of Expressions (수식의 계산) (0) | 2020.04.23 |
|---|---|
| 3-3강 - Mazing Problem (미로 문제) (0) | 2020.04.22 |
| 3-1강 - Stack, Stack using Dynamic Arrays (스택, 동적 배열로 만든 스택) (1) | 2020.04.21 |
| 2-5강 - Multidimensional Arrays, Strings (다차원 배열, 문자열) (0) | 2020.04.15 |
| 2-4강 - Sparse Matrix (희소 행렬) (0) | 2020.04.10 |



